题目内容
(本题满分14分)
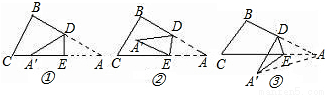
问题1如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是什么?
研究(2):如果折成图②的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是什么?
研究(3):如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.
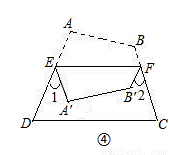
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是什么?
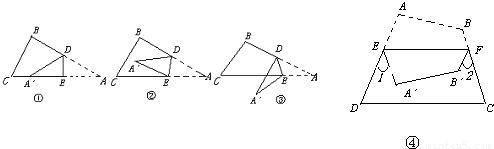
(1)∠BDA′=2∠A;(2)∠BDA′+∠CEA′=2∠A;(3)∠BDA′-∠CEA′=2∠A;
(4)∠1+∠2=2(∠A+∠B)-360°.
【解析】
试题分析:(1)根据三角形的外角的性质以及折叠的特点即可得到结论;
(2)连接AA′,根据三角形的外角的性质即可得到结论;
(3)连接AA′构造等腰三角形,然后结合三角形的外角性质进行探讨证明;
(4)根据平角的定义以及四边形的内角和定理进行探讨.
试题解析:(1)根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,故∠BDA′=2∠A;
(2)由图形折叠的性质可知,∠CEA′=180°-2∠DEA′…①,∠BDA′=180°-2∠A′DE…②,
①+②得,∠BDA′+∠CEA′=360°-2(∠DEA′+∠A′DE
即∠BDA′+∠CEA′=360°-2(180°-∠A),
故∠BDA′+∠CEA′=2∠A;
(3)∠BDA′-∠CEA′=2∠A.
证明如下:
连接AA′构造等腰三角形,
∠BDA′=2∠DA'A,∠CEA'=2∠EA'A,
得∠BDA'-∠CEA'=2∠A,
(4)如图④,由图形折叠的性质可知∠1=180°-2∠AEF,∠2=180°-2∠BFE,
两式相加得,∠1+∠2=360°-2(∠AEF+∠BFE)
即∠1+∠2=360°-2(360°-∠A-∠B),
所以,∠1+∠2=2(∠A+∠B)-360°.
考点:三角形内角和定理;三角形的外角性质;翻折变换(折叠问题).

 ,计算
,计算 得
得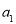 ;
;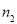 ,计算
,计算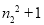 得
得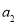 ;
;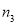 ,再计算
,再计算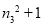 得
得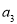 ;
;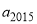 = .
= . 的系数为( )
的系数为( ) B.-2 C.
B.-2 C.  D.
D. 
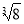 +
+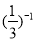 -
-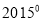 ; (2)已知:(x-1)2=9,求x的值.
; (2)已知:(x-1)2=9,求x的值.