题目内容
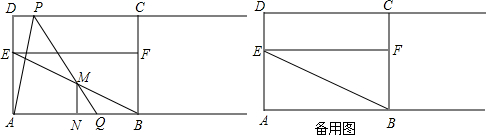
1.如图,在矩形ABCD中,AB=6,AD=$3\sqrt{3}$,点E是AD的三等分点,且AE>DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为t秒.(1)当点Q与点B重合时,求DP的长度;
(2)设AB的中点为N,PQ与线段BE相交于点M,是否存在点P,使△BMN为等腰三角形?若存在,请直接写出时间t的值;若不存在,请说明理由.
(3)设△APQ与四边形ABFE的重叠部分的面积为S,试求S与t的函数关系式和相应的自变量t的取值范围.
分析 (1)过点P作PH垂直于AB,特殊含30°的直角三角形求出HB,再求DP即可,
(2)分三种情况①当MN=BN=3时②当BM=BN=3时③当MN=MB时分别求解即可,
(3)①分三种情况当0≤t≤3时,Q在点B的左侧或重合时,②当3<t≤5时,即H点在F点的左侧或重合时,③当t>9,即点K在点F的右侧,分别求解即可.
解答 解:(1)如图1,过点P作PH垂直于AB,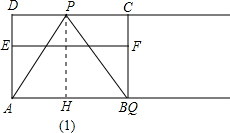
∵∠PQA=60°,AD=3$\sqrt{3}$,
∴PH=3$\sqrt{3}$,
∴$HB=CP=\frac{PH}{tan60°}=3$,
∴DP=DC-CP=6-3=3;
(2)存在存在点P,使△BMN为等腰三角形
①如图2,当MN=BN=3时,连接DM,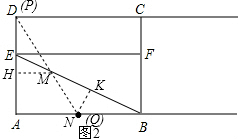
∵AB=6,AD=$3\sqrt{3}$,点E是AD的三等分点,且AE>DE,AB的中点为N,
∴AE=2$\sqrt{3}$,
∴∠ABE=30°,
∴∠ABE=∠BMN=30°BE=4$\sqrt{3}$
作NK⊥BE,交BE于点K,MH⊥AD,
∵BN=3,
∴MK=BK=$\frac{3\sqrt{3}}{2}$,
∴EM=$\sqrt{3}$,
∵△AEB∽△HEM,
∴$\frac{EM}{BE}$=$\frac{MH}{AN}$,即$\frac{\sqrt{3}}{4\sqrt{3}}$=$\frac{MH}{6}$,解得MH=$\frac{3}{2}$,
同理EH=$\frac{\sqrt{3}}{2}$,
∴DH=$\frac{3\sqrt{3}}{2}$,
∴∠HDM=30°,
∴DM、MN在一条直线上,即P点与D点重合,Q点与N点重合,
∴t=0时,存在点P,使△BMN为等腰三角形,
②如图3,当BM=BN=3时,过点M作KH⊥CD,交CD于点K,AB于点H,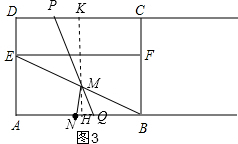
∵∠ABE=30°,
∴MH=$\frac{3}{2}$,BH=$\frac{3\sqrt{3}}{2}$,
∴KM=3$\sqrt{3}$-$\frac{3}{2}$,AH=6-$\frac{3\sqrt{3}}{2}$,
∵∠PQA=60°,
∴∠MPK=60°,
∴PK=$\frac{3\sqrt{3}-\frac{3}{2}}{\sqrt{3}}$=3-$\frac{\sqrt{3}}{2}$,
∴DP=AH-PK=DK-PK=6-$\frac{3\sqrt{3}}{2}$-(3-$\frac{\sqrt{3}}{2}$)=3-$\sqrt{3}$,
∴当t=3-$\sqrt{3}$时,存在点P,使△BMN为等腰三角形,
③如图4,当MN=MB时,过点M作KH⊥CD,交CD于点K,AB于点H,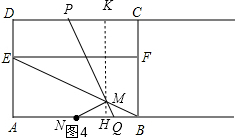
∵∠ABE=30°,
∴MH=$\frac{\sqrt{3}}{2}$,BH=$\frac{3}{2}$,
∴KM=3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$,AH=6-$\frac{3}{2}$=$\frac{9}{2}$,
∵∠PQA=60°,
∴∠MPK=60°,
∴PK=(3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$)÷$\sqrt{3}$=$\frac{5}{2}$,
∴DP=AH-PK=DK-PK=$\frac{9}{2}$-$\frac{5}{2}$=2,
∴当t=2时,存在点P,使△BMN为等腰三角形,
综上所述:t=0,t=3-$\sqrt{3}$,t=2时,存在点P,使△BMN为等腰三角形,
(3)设△APQ与四边形ABFE的重叠部分的面积为S,
①如图5,0≤t≤3,Q在点B的左侧或重合时,M为DC的中点,连接MB,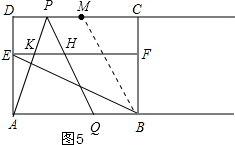
S=S△APQ-S△KHP=$\frac{1}{2}$AQ•AD-$\frac{1}{2}$KH•DE=$\frac{1}{2}$×[6-(3-t)]×3$\sqrt{3}$-$\frac{1}{2}$×$\frac{1}{3}$×[6-(3-t)]×$\sqrt{3}$=$\frac{4\sqrt{3}}{3}t$+4$\sqrt{3}$;
②如图6,当3<t≤5时,即H点在F点的左侧或重合时,M为DC的中点,连接MB,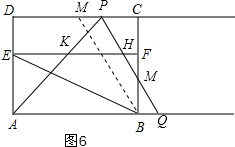
△APQ与四边形ABFE的重叠部分的面积
S=S△APQ-S△KHP-S△BQM=$\frac{1}{2}$AQ•AD-$\frac{1}{2}$KH•DE-$\frac{1}{2}$BQ•BM=$\frac{1}{2}$[6+(t-3)]×3$\sqrt{3}$-$\frac{1}{2}$×$\frac{1}{3}$[6+(t-3)]×$\sqrt{3}$-$\frac{1}{2}$(t-3)×$\sqrt{3}$(t-3)=-$\frac{\sqrt{3}}{2}$t2+$\frac{13\sqrt{3}}{3}$t-$\frac{\sqrt{3}}{2}$;
③如图7,当5<t≤9,即H点在F点的右侧,K点在F点的左侧时,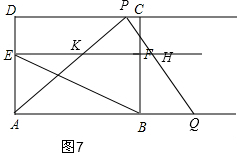
△APQ与四边形ABFE的重叠部分的面积S=S四边形ABFE-S△AKE=AB•AE-$\frac{1}{2}$EK•AE=6×2$\sqrt{3}$-$\frac{1}{2}$×$\frac{2}{3}$t×2$\sqrt{3}$=-$\frac{2\sqrt{3}}{3}t$+12$\sqrt{3}$;
③如图8,当t>9,即点K在点F的右侧,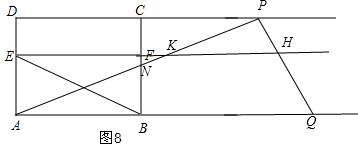
△APQ与四边形ABFE的重叠部分的面积S=S△ABN=$\frac{1}{2}$BN•AB=$\frac{1}{2}$×6×(3$\sqrt{3}$-$\frac{3\sqrt{3}(t-6)}{t}$)=$\frac{54\sqrt{3}}{t}$,
综上所述△APE与四边形ABFE的重叠部分的面积S=$\left\{\begin{array}{l}{\frac{4\sqrt{3}}{3}t+4\sqrt{3}(0≤t≤3)}\\{-\frac{\sqrt{3}}{2}{t}^{2}+\frac{13\sqrt{3}}{3}t-\frac{\sqrt{3}}{2}(3<t≤5)}\\{-\frac{2\sqrt{3}}{3}t+12\sqrt{3}(5<t≤9)}\\{\frac{54\sqrt{3}}{t}(t>9)}\end{array}\right.$.
点评 本题主要考查了四边形综合题,涉及相似三角形的性质,动点问题,平行四边形的性质及三角形,四边形的面积公式,解题的关键是正确的画出图形,分情况讨论,难度较大.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案| A. | $\frac{3}{10}$ | B. | $\frac{6}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{3}{5}$ |
| A. | 两条对角线相等 | B. | 两条对角线相互垂直 | ||
| C. | 两条对角线相互垂直平分 | D. | 两条对角线相等且垂直 |
| A. | 12 | B. | 6 | C. | 3 | D. | $\frac{3}{2}$ |

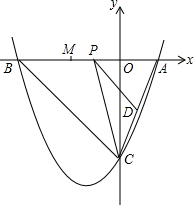 已知:如图,抛物线y=a(x+1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(2,0).
已知:如图,抛物线y=a(x+1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(2,0).