题目内容
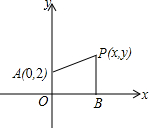 如图,点P(x,y)为平面直角坐标系内一点,PB⊥x轴,垂足为B,点A的坐标为(0,2),若PA=PB,则以下结论正确的是( )
如图,点P(x,y)为平面直角坐标系内一点,PB⊥x轴,垂足为B,点A的坐标为(0,2),若PA=PB,则以下结论正确的是( )A、点P在直线y=
| ||
B、点P在抛物线y=
| ||
C、点P在抛物线y=
| ||
D、点P在抛物线y=
|
考点:勾股定理,二次函数的性质
专题:
分析:由于点P(x,y),则点B(x,0),根据PA=PB,可得y与x之间的关系,依此即可求解.
解答:解:∵点P(x,y),
∴点B(x,0),
∵PA=PB,
∴y2=x2+(y-22),
∴y=
x2+1,
∴点P在抛物线y=
x2+1上.
故选:C.
∴点B(x,0),
∵PA=PB,
∴y2=x2+(y-22),
∴y=
| 1 |
| 4 |
∴点P在抛物线y=
| 1 |
| 4 |
故选:C.
点评:考查了二次函数的性质和两点之间的距离公式,解题的关键是根据PA=PB,得到y与x之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
我国以2011年11月1日零时为标准时点进行了第六次全国人口普查,普查得到全国总人口为1370536875人,该数用科学记数法表示并保留三位有效数字为( )
| A、1.37×109 |
| B、13.7×108 |
| C、1.4×109 |
| D、13.7 亿 |
若将函数y=3x2的图象向右平行移动1个单位,再向上平移5个单位,可得到的抛物线是( )
| A、y=3(x+1)2-5 |
| B、y=3(x+1)2+5 |
| C、y=3(x-1)2-5 |
| D、y=3(x-1)2+5 |
如果4x=3y,则
=( )
| 2x+y |
| 2x-y |
A、
| ||
| B、5 | ||
C、
| ||
D、
|
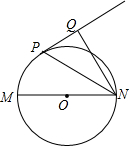 如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
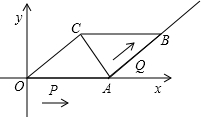 已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从0点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从0点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.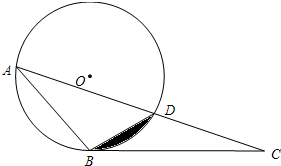 如图,△ABC中,⊙O经过A、B两点,且交AC于点D,∠DBC=∠BAC.
如图,△ABC中,⊙O经过A、B两点,且交AC于点D,∠DBC=∠BAC.