题目内容
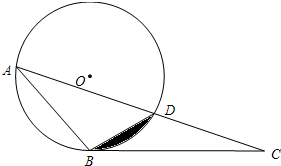 如图,△ABC中,⊙O经过A、B两点,且交AC于点D,∠DBC=∠BAC.
如图,△ABC中,⊙O经过A、B两点,且交AC于点D,∠DBC=∠BAC.(1)判断BC与⊙O有何位置关系,并说明理由;
(2)若⊙O的半径为4,∠BAC=30°,求图中阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)连接BO并延长交⊙O于点E,连接DE.由圆周角定理得出∠BDE=90°,再求出∠EBD+∠DBC=90°,根据切线的判定定理即可得出BC是⊙O的切线;
(2)分别求出等边三角形DOB的面积和扇形DOB的面积,即可求出答案.
(2)分别求出等边三角形DOB的面积和扇形DOB的面积,即可求出答案.
解答: 解:(1)BC是⊙O的切线.理由如下:
解:(1)BC是⊙O的切线.理由如下:
连接BO并延长交⊙O于点E,连接DE.
∵BE是⊙O的直径,
∴∠BDE=90°,
∴∠EBD+∠E=90°,
∵∠DBC=∠DAB,∠DAB=∠E,
∴∠EBD+∠DBC=90°,
即OB⊥BC,
又∵点B在⊙O上,
∴BC是O的切线;
(2)∵∠BOD=2∠A=60°,OB=OD,
∴△BOD是边长为4的等边三角形,
∴S△BOD=
×42=4
,
∵S扇形DOB=
=
π,
∴S阴影=S扇形DOB-S△BOD=
π-4
.
 解:(1)BC是⊙O的切线.理由如下:
解:(1)BC是⊙O的切线.理由如下:连接BO并延长交⊙O于点E,连接DE.
∵BE是⊙O的直径,
∴∠BDE=90°,
∴∠EBD+∠E=90°,
∵∠DBC=∠DAB,∠DAB=∠E,
∴∠EBD+∠DBC=90°,
即OB⊥BC,
又∵点B在⊙O上,
∴BC是O的切线;
(2)∵∠BOD=2∠A=60°,OB=OD,
∴△BOD是边长为4的等边三角形,
∴S△BOD=
| ||
| 4 |
| 3 |
∵S扇形DOB=
| 60π×42 |
| 360 |
| 8 |
| 3 |
∴S阴影=S扇形DOB-S△BOD=
| 8 |
| 3 |
| 3 |
点评:本题考查了切线的判定,圆周角定理,扇形面积,等边三角形的性质和判定的应用,关键是求出∠EBD+∠DBC=90°和分别求出扇形DOB和三角形DOB的面积.

练习册系列答案
相关题目
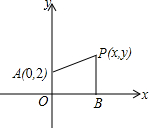 如图,点P(x,y)为平面直角坐标系内一点,PB⊥x轴,垂足为B,点A的坐标为(0,2),若PA=PB,则以下结论正确的是( )
如图,点P(x,y)为平面直角坐标系内一点,PB⊥x轴,垂足为B,点A的坐标为(0,2),若PA=PB,则以下结论正确的是( )A、点P在直线y=
| ||
B、点P在抛物线y=
| ||
C、点P在抛物线y=
| ||
D、点P在抛物线y=
|
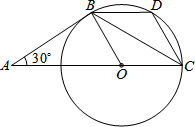 如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=AD=4,D为QP的中点.
如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=AD=4,D为QP的中点. 如图,某居民楼A与公路MN相距60m(AB=60m),在公路MN上行驶的汽车在距居民楼A100m的点P处就可使其受到噪音的影响,求在公路上以10m/s的速度行驶的汽车给居民楼A的居民带来多长时间的噪音影响.
如图,某居民楼A与公路MN相距60m(AB=60m),在公路MN上行驶的汽车在距居民楼A100m的点P处就可使其受到噪音的影响,求在公路上以10m/s的速度行驶的汽车给居民楼A的居民带来多长时间的噪音影响.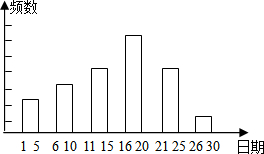 某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答:
某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答: