题目内容
已知直线y=2x+4与x轴的交点为A,与y轴的交点为B,点C(a,0)是x轴正半轴上一动点.
(1)试写出△ABC的面积S与a的关系式,并求出当a为何值时S△ABC=S△AOB;
(2)若M(1,3)是线段BC上一点,求△ABM的面积.
(1)试写出△ABC的面积S与a的关系式,并求出当a为何值时S△ABC=S△AOB;
(2)若M(1,3)是线段BC上一点,求△ABM的面积.
考点:一次函数图象上点的坐标特征
专题:计算题
分析:(1)先确定A(-2,0),B(0,4),再利用三角形面积公式得到S与a的关系式,由于点C(a,0)是x轴正半轴上一动点,则无论a取何值,都没有S△ABC=S△AOB;
(2)先利用待定系数法求出直线BC的解析式为y=-x+4,再确定C点坐标,然后利用△ABM的面积=△ABC的面积-△MAC的面积进行计算.
(2)先利用待定系数法求出直线BC的解析式为y=-x+4,再确定C点坐标,然后利用△ABM的面积=△ABC的面积-△MAC的面积进行计算.
解答: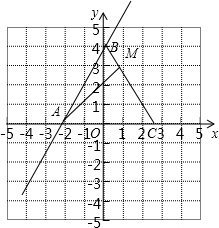 解:(1)∵直线y=2x+4与x轴的交点为A,与y轴的交点为B,
解:(1)∵直线y=2x+4与x轴的交点为A,与y轴的交点为B,
∴A(-2,0),B(0,4),
∴S=
•(a+2)•4=2a+4;
∵点C(a,0)是x轴正半轴上一动点,
∴无论a取何值,都没有S△ABC=S△AOB;
(2)设直线BC的解析式为y=kx+b,
把B(0,4)、C(1,3)代入得
,解得
,
所以直线BC的解析式为y=-x+4,
所以C点坐标为(4,0),
所以△ABM的面积=△ABC的面积-△MAC的面积
=
•4•6-
•3•6
=3.
 解:(1)∵直线y=2x+4与x轴的交点为A,与y轴的交点为B,
解:(1)∵直线y=2x+4与x轴的交点为A,与y轴的交点为B,∴A(-2,0),B(0,4),
∴S=
| 1 |
| 2 |
∵点C(a,0)是x轴正半轴上一动点,
∴无论a取何值,都没有S△ABC=S△AOB;
(2)设直线BC的解析式为y=kx+b,
把B(0,4)、C(1,3)代入得
|
|
所以直线BC的解析式为y=-x+4,
所以C点坐标为(4,0),
所以△ABM的面积=△ABC的面积-△MAC的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=3.
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b).
直线上任意一点的坐标都满足函数关系式y=kx+b.
直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
在实数-
,0,
,π,
中,无理数有( )
| 22 |
| 7 |
| 4 |
| 3 | 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
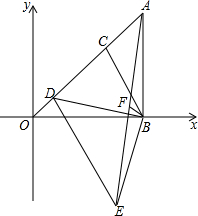 直角坐标系中,直线OC和BC的函数关系式分别是y=x,y=-2x+6,过B点作x轴的垂线交直线OC于A点,D是线段OC上的一个动点(点D,O不重合),以BD为直角边作等腰Rt△BDE(E在第四象限),F是AE中点.确定线段BF、AD的数量关系和位置关系,并加以证明.
直角坐标系中,直线OC和BC的函数关系式分别是y=x,y=-2x+6,过B点作x轴的垂线交直线OC于A点,D是线段OC上的一个动点(点D,O不重合),以BD为直角边作等腰Rt△BDE(E在第四象限),F是AE中点.确定线段BF、AD的数量关系和位置关系,并加以证明.