Question

4．在矩形ABCD中，AB=3厘米，AD=4厘米，点P以每秒$\frac{4}{5}$厘米的速度在BC上从B往C运动，同时点Q以每秒1厘米的速度在CA上从C往A运动，设运动时间为t秒．
（1）当PQ平行于AB时，求t的值；
（2）是否存在某一时刻t，使点P、Q、D三点在同一直线上？若存在，求出t；若不存在，请说明理由；
（3）当△PQC为等腰三角形时，求t的值．

Answer 1

分析 （1）根据勾股定理求出AC的长，根据平行线分线段成比例定理列出比例式，计算即可；
（2）根据相似三角形的性质得到$\frac{CQ}{CA}$=$\frac{CP}{CB}$，代入数据计算即可；
（3）分CQ=CP、QP=QC、PQ=PC三种情况，根据等腰三角形的性质和相似三角形的性质进行计算即可．

解答 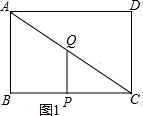解：（1）∵∠B=90°，AB=3厘米，AD=4厘米，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5厘米，
由题意得，BP=$\frac{4}{5}$t，CQ=t，则CP=4-$\frac{4}{5}$t，
∵PQ∥AB，
∴$\frac{CQ}{CA}$=$\frac{CP}{CB}$，即$\frac{t}{5}$=$\frac{4-\frac{4}{5}t}{4}$，
解得t=$\frac{5}{2}$；
（2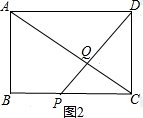）∵四边形ABCD为矩形，
∴AD∥BC，
如图2，当点P、Q、D三点在同一直线上时，$\frac{PC}{AD}$=$\frac{CQ}{AQ}$，即$\frac{4-\frac{4}{5}t}{4}$=$\frac{t}{5-t}$，
解得t₁=$\frac{15+5\sqrt{5}}{2}$（舍去），t₂=$\frac{15-5\sqrt{5}}{2}$，
则当t=$\frac{15-5\sqrt{5}}{2}$时，点P、Q、D三点在同一直线上；
（3）当CQ=CP时，4-$\frac{4}{5}$t=t，
解得t=$\frac{20}{9}$；
当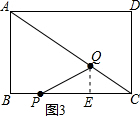QP=QC时，
如图3，作QE⊥BC于E，
则PE=EC=$\frac{1}{2}$（4-$\frac{4}{5}$t），
∵QE∥AB，
∴$\frac{CE}{CB}$=$\frac{CQ}{CA}$，
即$\frac{2-\frac{2}{5}t}{4}$=$\frac{t}{5}$，
解得t=$\frac{5}{3}$；
当PQ=PC时，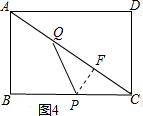
如图4，作PF⊥AC于F，
则FC=$\frac{1}{2}$QC=$\frac{1}{2}$t，
∵PF⊥AC，∠B=90°，
∴△CFP∽△CBA，
∴$\frac{CF}{CB}$=$\frac{CP}{CA}$，即$\frac{\frac{1}{2}t}{4}$=$\frac{4-\frac{4}{5}t}{5}$，
解得t=$\frac{160}{57}$，
综上所述，t=$\frac{20}{9}$或t=$\frac{5}{3}$或t=$\frac{160}{57}$时，△PQC为等腰三角形．

点评 本题考查的是矩形的性质、等腰三角形的判定和性质、相似三角形的性质的应用，正确作出辅助线、灵活运用相关定理和分情况讨论思想是解题的关键．