题目内容
12. 如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P.
如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P.(1)求∠APE的度数;
(2)连接CP,若CP⊥AD,求BP:AP的值.
分析 (1)根据等边三角形的性质得到∠ABD=∠C,AB=BC,推出△ABD≌△BCE,根据全等三角形的性质得到∠BAD=∠CBE,由于∠ABE+∠EBC=60°,求得∠APE=∠ABE+∠BAD=60°,即可得到结论;
(2)延长AP到F使PF=BP,连接CF,得到△PBF是等边三角形,由等边三角形的性质得到∠PBF=∠ABC=60°,求得∠ABP=∠CBF,推出△ABP≌△BCF,根据全等三角形性质得到CF=AP,∠BAP=∠BCF,太迟A,B,F,C四点共圆,根据圆周角定理得到∠AFC=∠ABC=60°,根据直角三角形的性质即可得到结论.
解答 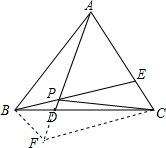 解:(1)∵△ABC是等边三角形,
解:(1)∵△ABC是等边三角形,
∴∠ABD=∠C,AB=BC,
在△ABD与△BCE中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE,
∴∠BAD=∠CBE,
∵∠ABE+∠EBC=60°,
∴∠APE=∠ABE+∠BAD=60°,
∴∠APE=60°;
(2)延长AP到F使PF=BP,连接CF,
∵∠BPF=∠APE=60°,
∴△PBF是等边三角形,
∴∠PBF=∠ABC=60°,
∴∠ABP=∠CBF,
在△ABP与△CBF中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABP=∠CBF}\\{BP=BF}\end{array}\right.$,
∴△ABP≌△BCF,
∴CF=AP,∠BAP=∠BCF,
∴A,B,F,C四点共圆,
∴∠AFC=∠ABC=60°,
∵∠CPF=90°,
∴∠PCF=30°,
∴PF=$\frac{1}{2}$CF,
∴PB=$\frac{1}{2}$AP,即PB:AP=$\frac{1}{2}$.
点评 本题考查了全等三角形的判定和性质,等边三角形的判定和性质,直角三角形的性质,四点共圆,正确的作出辅助线是解题的关键.

 如图,⊙O是△ABC的外接圆,连接OA、OB,∠AOB=50°,则∠C的度数为( )
如图,⊙O是△ABC的外接圆,连接OA、OB,∠AOB=50°,则∠C的度数为( )| A. | 25° | B. | 40° | C. | 50° | D. | 80° |

 如图表示两辆汽车行驶路程与时间的关系(汽车B在汽车A后出发)的图象,试回答下列问题:
如图表示两辆汽车行驶路程与时间的关系(汽车B在汽车A后出发)的图象,试回答下列问题: 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且$\widehat{AB}$=60°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径为6,则GE+FH的最大值为9.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且$\widehat{AB}$=60°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径为6,则GE+FH的最大值为9. 如图,在平面直角坐标系中,抛物线的解析式为y=-x2+2x+5,点A为抛物线上一点,且坐标为(-1,a).
如图,在平面直角坐标系中,抛物线的解析式为y=-x2+2x+5,点A为抛物线上一点,且坐标为(-1,a). 如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x. 在矩形ABCD中,AB=3厘米,AD=4厘米,点P以每秒$\frac{4}{5}$厘米的速度在BC上从B往C运动,同时点Q以每秒1厘米的速度在CA上从C往A运动,设运动时间为t秒.
在矩形ABCD中,AB=3厘米,AD=4厘米,点P以每秒$\frac{4}{5}$厘米的速度在BC上从B往C运动,同时点Q以每秒1厘米的速度在CA上从C往A运动,设运动时间为t秒.