��Ŀ����
����Ŀ����ͼ����֪A��B��C��DΪ���ε��ĸ����㣬AB��16 cm��AD��6 cm������P��Q�ֱ�ӵ�A��Cͬʱ��������P��3 cm/s���ٶ����B�ƶ���һֱ����BΪֹ����Q��2 cm/s���ٶ����D�ƶ�������Pֹͣ�˶�ʱ����QҲֹͣ�˶����ʣ�
(1)P��Q����ӿ�ʼ�����ʱ��ʱ���ı���PBCQ�������33 cm2?
(2)P��Q����ӿ�ʼ�����ʱ��ʱ����P���Q֮��ľ�����10 cm?
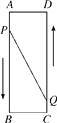
���𰸡�(1) P��Q����ӿ�ʼ����5sʱ���ı���PBCQ�������33cm2��(2) P��Q����ӿ�ʼ����1.6s��4.8sʱ����P���Q֮��ľ�����10cm.
�����������������(1)��������xsʱ���Ϊ33��Ȼ��������ε�������㷨���г����̣��Ӷ�����𰸣�(2)������Q��QH��AB��H��Ȼ�����PH�ij��ȣ�������Rt��PHQ�Ĺ��ɶ������δ֪����ֵ�ó��𰸣�
����������⣺(1)��P��Q����ӿ�ʼ����xsʱ���ı���PBCQ�������33cm2.
���������![]() ��(16��3x��2x)��6��33��
��(16��3x��2x)��6��33��
���x��5.(3��)��16��3��![]() >5��
>5��
��x��5�������⣮
��P��Q����ӿ�ʼ����5sʱ���ı���PBCQ�������33cm2��
(2)��P��Q����ӿ�ʼ����ysʱ����P��Q֮��ľ�����10cm��
����Q��QH��AB��H��

���QHA��90��.���ı���ABCD�Ǿ��Σ����A����D��90����
���ı���ADQH�Ǿ��Σ���AH��DQ��(16��2y)cm��QH��AD��6cm��
�൱P����H���Ϸ�ʱ��PH��AH��AP��16��2y��3y��(16��5y)(cm)����P����H���·�ʱ��PH��AP��AH��3y��(16��2y)��(5y��16)(cm)�� ��PH��|16��5y|cm.
��Rt��PQH�У����ݹ��ɶ�����PH2��QH2��PQ2��
��(16��5y)2��62��102�����y1��1.6��y2��4.8. ��16��3��![]() ��
��
��y1��1.6��y2��4.8���������⣮
��P��Q����ӿ�ʼ����1.6s��4.8sʱ����P���Q֮��ľ�����10cm��

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�����Ŀ��Ϊ��ʵ�������˸���������������������ȫ�淢չ���������Ӱ��ˣ�����ѧУ������ѧ����ѧ��ʱ�涨��ÿѧ�ڶ�ѧ���ĵ������������������������ۺ��������ۣ��ֱ��ǣ������ۺ��������ۡ������ۺ��������ۡ���ĩ�ۺ��������ۣ����꼶��1�����С���Ͱ��꼶��2�����С����λͬѧͬʱ����һ�Ƚ�ѧ����������ǵ������ۺ��������۳ɼ����±���
�����ۺ��������۳ɼ� | �����ۺ��������۳ɼ� | ��ĩ�ۺ��������۳ɼ� | |
�� | 96 | 91 | 92 |
�� | 95 | 93 | 91 |
��1������������ۺ��������۳ɼ��ȶ��ԵĽǶ�������˭���Ե�һ�Ƚ�ѧ������ͨ������ش�
��2����������ۺ��������۳ɼ��������ۺ��������۳ɼ�����ĩ�ۺ��������۳ɼ���![]() �ı����������ճɼ���˭���Ե�һ�Ƚ�ѧ������ͨ������ش�
�ı����������ճɼ���˭���Ե�һ�Ƚ�ѧ������ͨ������ش�