题目内容
【题目】如图,A点的坐标为(0,3),B点的坐标为(-3.0),D为x轴上的一个动点,AE⊥AD,且AE=AD,连接BE交y轴于点M
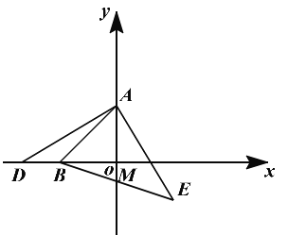
(1)若D点的坐标为(-5.0),求E点的坐标:
(2)求证:M为BE的中点
(3)当D点在x轴上运动时,探索:![]() 为定值
为定值
【答案】(1)E(3,-2);(2)详见解析;(3)![]()
【解析】
(1) 过E点作EF⊥y轴交y轴于F点,先证明△AOD≌△EFA(AAS),根据全等三角形的性质即可得到E点的坐标;
(2)先把D点的位置画出来,再证明△AOD≌△EFA(AAS),再根据全等三角形的性质证明△BOM≌△EFM(AAS),即可证明M为BE的中点;
(3)从(1)(2)的信息可知得到![]() ,再结合
,再结合![]() 即可得到
即可得到![]() 的比值为定值;
的比值为定值;
(1) 过E点作EF⊥y轴交y轴于F点
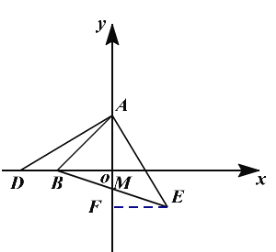
∵AD⊥AE , EF⊥AF
∠AOD=∠AFE=90°
∵∠DAO+∠EAF=90°
∠EAF+∠AEF=90°
∴∠DAO=∠AEF
在△AOD和△EFA中
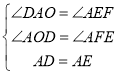
△AOD≌△EFA(AAS)
EF=OA=3 AF=OD=5
OF=AF-OA=5-3=2
E(3,-2)
(2)
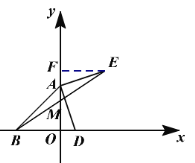
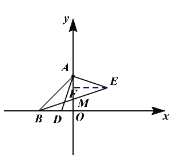

D点在以上3个位置,
根据题意知道:AE=AD,![]() ,
,
又∵ ![]() ,
,
∴![]()
∴△AOD≌△EFA(AAS)
∴OB=EF ∠BOM=∠EMF=90°
∠BOM=∠EMF
∴△BOM≌△EFM(AAS)
BM=EM=![]() BE
BE
(3) 根据(2)可知,D点在可以在3个位置,
当D点如下图的位置时,过D作直线a⊥x轴与D,过A作AG垂直直线a于G,
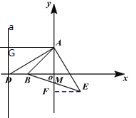
由(2)知△BOM≌△EFM(AAS),
∴EF=OB,
又由(1)知△AOD≌△EFA(AAS)
即:EF=OA =OB,AF=OD
∴![]() ,
,
又∵![]()
∴![]() =
=![]() ,
,
当D在另外两个位置时,同理可证得![]() =
=![]() ;
;

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】七(1)班同学为了解2017年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量 | 频数(户数) | 百分比 |
| 6 |
|
|
| |
| 16 |
|
| 10 |
|
| 4 | |
| 2 |
|

(1)请将下列频数分布表和频数分布直方图补充完整;
(2)求该小区月均用水量不超过![]() 的家庭占被调查家庭总数的百分比;
的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过![]() 的家庭数.
的家庭数.