题目内容
【题目】某中学为了丰富学生的课余生活,准备从体育用品商店一次性购买若干个排球和篮球,若购买2个排球和1个篮球共需190元.购买3个排球和2个篮球共需330元.
(1)购买一个排球、一个篮球各需多少元?
(2)根据该校的实际情况,需从体育用品商店一次性购买排球和篮球共100个,要求购买排球和篮球的总费用不超过6500元,这所中学最多可以购买多少个篮球?
【答案】(1)购买一个排球需50元、一个篮球需90元;(2)这所中学最多可以购买37个篮球.
【解析】
(1)设每个排球x元,每个篮球y元,根据“购买2个排球和1个篮球共需190元,购买3个排球和2个篮球共需330元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买篮球a个,则购买排球(100-a)个,根据总价=单价×数量结合购买排球和篮球的总费用不超过6500元,即可得出关于a的一元一次不等式,解之取其中的最大值整数值即可得出结论.
解:(1)设每个排球x元,每个篮球y元,
依题意,得:![]()
解得:![]()
答:每个排球50元,每个篮球90元.
(2)设购买篮球a个,则购买排球(100-a)个,
依题意,得:90a+50(100-a)≤6500,
解得:a≤37.5.
∵a为整数,
∴a最大取37.
答:最多可以买37个篮球.

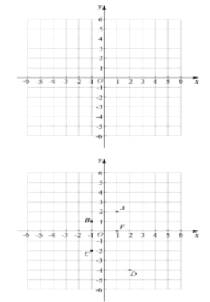
【题目】如图,在方格纸内将![]() 经过一次平移后得到
经过一次平移后得到![]() ,图中标出了点
,图中标出了点![]() 的对应点
的对应点![]() .(小正方形边长为1,
.(小正方形边长为1,![]() 的顶点均为小正方形的顶点)
的顶点均为小正方形的顶点)
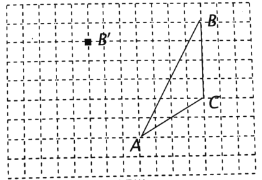
(1)补全![]() ;
;
(2)画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 中
中![]() 边上的高线
边上的高线![]() ;
;
(4)![]() 的面积为_____.
的面积为_____.
【题目】七(1)班同学为了解2017年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量 | 频数(户数) | 百分比 |
| 6 |
|
|
| |
| 16 |
|
| 10 |
|
| 4 | |
| 2 |
|

(1)请将下列频数分布表和频数分布直方图补充完整;
(2)求该小区月均用水量不超过![]() 的家庭占被调查家庭总数的百分比;
的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过![]() 的家庭数.
的家庭数.