题目内容
8.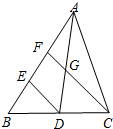 如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,连接DE,CF交AD于G,点E是BF中点.
如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,连接DE,CF交AD于G,点E是BF中点.(1)求证:△AFG∽△AED
(2)若FG=2,G为AD中点,求CG的长.
分析 (1)根据AD是BC边上的中线,点E是BF中点,得到BD=CD,BE=EF,根据三角形的中位线的性质得到DE∥CF,即可得到结论;
(2)由G为AD中点,FG∥DE,得到AF=EF,求得DE=2FG=4,根据三角形的中位线的性质得到CF=2DE=8,即可得到结论.
解答 (1)证明:∵AD是BC边上的中线,点E是BF中点,
∴BD=CD,BE=EF,
∴DE是△BCF的中位线,
∴DE∥CF,
∴DE∥FG,
∴△AFG∽△AED;
(2)解:∵G为AD中点,FG∥DE,
∴AF=EF,
∴FG是△ADE的中位线,
∴DE=2FG=4,
∴CF=2DE=8,
∴CG=FC-FG=8-2=6.
点评 本题考查了相似三角形的判定和性质,三角形的中位线的性质,平行线等分线段定理,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
19.某县教育局为了解某校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表

(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中生人数.
某校初中生阅读数学教科书情况统计图表
| 类别 | 人数 | 占总人数比例 |
| 重视 | a | 0.3 |
| 一般 | 57 | 0.38 |
| 不重视 | b | c |
| 说不清楚 | 9 | 0.06 |

(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中生人数.
3.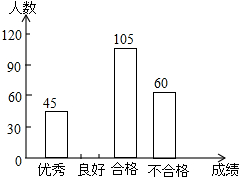 为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:
为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:
请结合图表所给出的信息解答下列问题:
(1)该校初二学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
 为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:
为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
(1)该校初二学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
18.点A为直线l外一点,点B在直线l上,若AB=3厘米,则点A到直线l的距离( )
| A. | 大于3厘米 | B. | 等于3厘米 | C. | 小于3厘米 | D. | 小于或等于3厘米 |
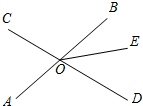 如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.
如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE. 小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人在1至3层的任意一层出电梯.
小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人在1至3层的任意一层出电梯. 程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.
程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.