题目内容
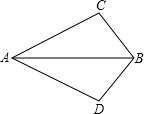 如图,AB平分∠DAC,要用SAS条件确定△ABC≌△ABD,还需要有条件( )
如图,AB平分∠DAC,要用SAS条件确定△ABC≌△ABD,还需要有条件( )分析:根据角平分线得出∠CAB=∠DAB,隐含条件AB=AB,根据全等三角形的判定定理判断即可.
解答:解:∵AB平分∠DAC,
∴∠CAB=∠DAB,
A、根据DB=CB,BA=BA,∠CAB=∠DAB不能推出两三角形全等,故本选项错误;
B、根据BA=BA,∠CAB=∠DAB不能推出两三角形全等,故本选项错误;
C、∵在△CAB和△DAB中
,
∴△CAB≌△DAB(SAS),故本选项正确;
D、根据BA=BA,∠CAB=∠DAB,∠D=∠C,根据AAS可证△CAB≌△DAB,根据本选项错误;
故选C.
∴∠CAB=∠DAB,
A、根据DB=CB,BA=BA,∠CAB=∠DAB不能推出两三角形全等,故本选项错误;
B、根据BA=BA,∠CAB=∠DAB不能推出两三角形全等,故本选项错误;
C、∵在△CAB和△DAB中
|
∴△CAB≌△DAB(SAS),故本选项正确;
D、根据BA=BA,∠CAB=∠DAB,∠D=∠C,根据AAS可证△CAB≌△DAB,根据本选项错误;
故选C.
点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 7、如图,AB为半圆直径,D为AB上一点,分别在半圆上取点E、F,使EA=DA,FB=DB,过D作AB的垂线,交半圆于C.
7、如图,AB为半圆直径,D为AB上一点,分别在半圆上取点E、F,使EA=DA,FB=DB,过D作AB的垂线,交半圆于C. 21、如图,BD平分∠ABC,DA⊥AB,∠1=60°,∠BDC=80°,求∠C的度数.
21、如图,BD平分∠ABC,DA⊥AB,∠1=60°,∠BDC=80°,求∠C的度数. (2012•上城区二模)如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,交OC于点E,连接CD,OD.给出以下四个结论:①S△DEC=
(2012•上城区二模)如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,交OC于点E,连接CD,OD.给出以下四个结论:①S△DEC= 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下四个结论:①S△AEC=2S△DEO;②AC=2CD;③线段OD是DE与DA的比例中项;④2CD2=CE•AB.其中正确结论的序号是
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下四个结论:①S△AEC=2S△DEO;②AC=2CD;③线段OD是DE与DA的比例中项;④2CD2=CE•AB.其中正确结论的序号是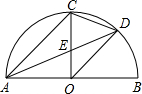 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连接CD、OD,给出以下5个结论:①OD∥AC;②AC=2CD;③CE=OE;④S△AEC=2S△DEO;⑤线段OD是DE与DA的比例中项;其中正确结论的序号是
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连接CD、OD,给出以下5个结论:①OD∥AC;②AC=2CD;③CE=OE;④S△AEC=2S△DEO;⑤线段OD是DE与DA的比例中项;其中正确结论的序号是