题目内容
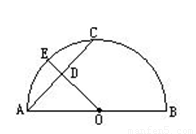
7、如图，AB为半圆直径，D为AB上一点，分别在半圆上取点E、F，使EA=DA，FB=DB，过D作AB的垂线，交半圆于C．求证：CD平分EF．
分析：为证明CD平分EF，想到可先证CD平分GH．为此添加CD的两条平行线EG、FH，从而得到G、H两点，从而利用射影定理可得DB2=FB2=AB•HB，AD2=AE2=AG•AB，两式相减后可得出结论．
解答：证明：如图，分别过点E、F作AB的垂线，G、H为垂足，连FA、EB．
易知：DB2=FB2=AB•HB，AD2=AE2=AG•AB．
二式相减得：DB2-AD2=AB•（HB-AG），
或（DB-AD）•AB=AB•（HB-AG）．
于是：DB-AD=HB-AG，或DB-HB=AD-AG．
∴DH=GD．
显然，EG∥CD∥FH．
故CD平分EF．
易知：DB2=FB2=AB•HB，AD2=AE2=AG•AB．
二式相减得：DB2-AD2=AB•（HB-AG），
或（DB-AD）•AB=AB•（HB-AG）．
于是：DB-AD=HB-AG，或DB-HB=AD-AG．
∴DH=GD．
显然，EG∥CD∥FH．
故CD平分EF．
点评：本题考查射影定理的知识及圆周角定理，难度较大，关键是掌握一些基本的知识，这是解答在综合题目的基础．
练习册系列答案
相关题目
如图，AB为半圆直径，O为圆心，C为半圆上一点，E是弧AC的中点，OE交弦AC于点D，若AC=8cm，DE=2cm，求OD的长．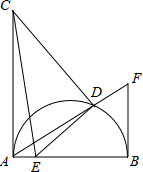
如图，AB为半圆直径，AC⊥AB，BF⊥AB，BF=2，AB=3，CA=4，连接AF交半圆于D，连接CD，作DE⊥CD交直径AB于E，则tan∠ACE=
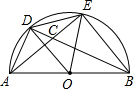如图，AB为半圆直径，D、E为圆周上两点，且AD=DE，AE与BD交于点C，则图中与∠BCE相等的角有（ ）