题目内容
如图2714,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.

证明:∵AB是⊙O的直径,
∴∠ACB=90°.
又∵CD⊥AB于点D,∴∠BCD=∠A.
又∵∠A=∠F(同弧所对的圆周角相等),
∴∠F=∠BCD=∠BCG.
在△BCG和△BFC中,

∴△BCG∽△BFC.∴ =
= .
.
即BC2=BG·BF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
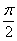 C.
C.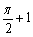 D.
D.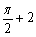
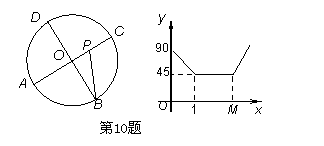
 =
= B.
B.

 =________.
=________.
 C.
C. D.5xy-5yx=0
D.5xy-5yx=0  是一个两位数,
是一个两位数, 是一个一位数,如果把
是一个一位数,如果把 B.
B.
 长是( )
长是( )







 为6厘米,则树的实际高度大约是(
为6厘米,则树的实际高度大约是(