题目内容
7. 如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
分析 据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.
解答 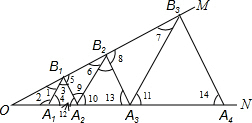 解:∵△A1B1A2是等边三角形,
解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°-120°-30°=30°,
又∵∠3=60°,
∴∠5=180°-60°-30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
…
∴△AnBnAn+1的边长为 2n-1,
∴△A9B9A10的边长为29-1=28=256.
故选D.
点评 本题考查的是等边三角形的性质以及等腰三角形的性质,根据已知得出A3B3=4B1A2,A4B4=8B1A2,A5B5=16B1A2进而发现规律是解题关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
17.下列命题中是假命题的是( )
| A. | 对顶角相等 | B. | 同位角相等 | ||
| C. | 邻补角互补 | D. | 平行于同一条直线的两条直线平行 |
16.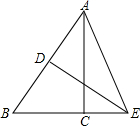 如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
 如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )| A. | $\frac{7}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{3}$ |
17. 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切 | D. | 以上三种情况均有可能 |
 如图,已知△ABC中,AB=2,BC=4
如图,已知△ABC中,AB=2,BC=4 如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(-1,-2),解答以下问题:
如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(-1,-2),解答以下问题: 如图,在数轴上表示-1,-$\sqrt{2}$的对应点分别是A,B,若点A是线段BC的中点,则C点表示的数为$\sqrt{2}$-2.
如图,在数轴上表示-1,-$\sqrt{2}$的对应点分别是A,B,若点A是线段BC的中点,则C点表示的数为$\sqrt{2}$-2.