Question

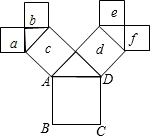
如图，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形a，b，c，d，e，f的面积和为32，则最大的正方形ABCD的边长为__________．

Answer 1

4．

【考点】勾股定理．

【分析】根据勾股定理得出a+b=c，e+f=d，c+d=S_{正方形ABCD}，由此可得出最大的正方形ABCD的面积，进而可得出其边长．

【解答】解：∵所有的四边形都是正方形，所有的三角形都是直角三角形，

∴a+b=c，e+f=d，c+d=S_{正方形ABCD}，

∵a+b+c+d+e+f=32，即2（c+d）=32，解得c+d=16，

∴S_{正方形ABCD}=16，

∴正方形ABCD的边长为4．

故答案为：4．

【点评】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．