题目内容
20.菱形的两条对角线分别是12和16,则此菱形的边长是( )| A. | 10 | B. | 8 | C. | 6 | D. | 5 |
分析 首先根据题意画出图形,然后由菱形的两条对角线的长分別为12cm和16cm,求得OA与OB,再由勾股定理即可求得菱形的边长.
解答 解:如图,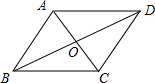
∵菱形ABCD中,AC=12cm,BD=16cm,
∴OA=$\frac{1}{2}$AC=6cm,OB=$\frac{1}{2}$BD=8cm,AC⊥BD,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=10(cm).
即菱形的边长是10cm.
故选A.
点评 此题考查了菱形的性质以及勾股定理.掌握菱形的对角线互相平分且垂直是解题的关键.

练习册系列答案
相关题目
10.将28°42′31″保留到“′”为( )
| A. | 28°42′ | B. | 28°43′ | C. | 28°42′30″ | D. | 29°00′ |
8. 一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
 一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )| A. | x≥2 | B. | x≤2 | C. | x≥4 | D. | x≤4 |
15.要使$\sqrt{x-1}$有意义,则x的取值范围是( )
| A. | x<1 | B. | x≥1 | C. | x≤-1 | D. | x<-1 |
9.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
则这些运动员成绩的中位数、众数分别为( )
| 成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 2 | 3 | 2 | 3 | 4 | 1 |
| A. | 1.65、1.70 | B. | 1.65、1.75 | C. | 1.70、1.75 | D. | 1.70、1.70 |
10. 如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=$\sqrt{5}$,∠EAF=135°,则以下结论正确的是( )
如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=$\sqrt{5}$,∠EAF=135°,则以下结论正确的是( )
 如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=$\sqrt{5}$,∠EAF=135°,则以下结论正确的是( )
如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=$\sqrt{5}$,∠EAF=135°,则以下结论正确的是( )| A. | DE=1 | B. | tan∠AFO=$\frac{1}{3}$ | ||
| C. | AF=$\frac{\sqrt{10}}{2}$ | D. | 四边形AFCE的面积为$\frac{9}{4}$ |
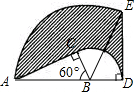 如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是36πcm2.(结果保留π).
如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是36πcm2.(结果保留π).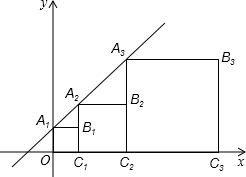 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3和C1,C2,C3,…分别在直线y=x+1和x轴上,则点
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3和C1,C2,C3,…分别在直线y=x+1和x轴上,则点