题目内容
5.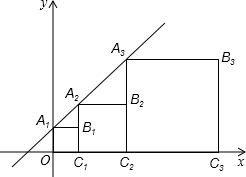 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3和C1,C2,C3,…分别在直线y=x+1和x轴上,则点
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3和C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2018的纵坐标是22017.
分析 根据一次函数图象上点的坐标特征结合正方形的性质即可得出点B1、B2、B3、…的坐标,根据点坐标的变化找出点Bn的坐标,依此即可得出结论.
解答 解:当x=0时,y=x+1=1,
∴点A1的坐标为(0,1).
∵A1B1C1O为正方形,
∴点C1的坐标为(1,0),点B1的坐标为(1,1).
同理,可得:B2(3,2),B3(7,4),B4(15,8),
∴点Bn的坐标为(2n-1,2n-1),
∴点B2018的坐标为(22018-1,22017).
故答案为:22017.
点评 本题考查了一次函数图象上点的坐标特征、正方形的性质以及规律型中点的坐标,根据点坐标的变化找出变化规律“点Bn的坐标为(2n-1,2n-1)”是解题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
15.甲、乙两名射箭运动员在某次测试中各射箭10次,两人的测试成绩如下表,则这两个人本次测试成绩的方差比较( )
| 甲的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 3 | 2 | 2 | 3 |
| 乙的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 2 | 3 | 3 | 2 |
| A. | S甲<S乙 | B. | S甲=S乙 | C. | S甲>S乙 | D. | 无法比较 |
16.下列图案中既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.菱形的两条对角线分别是12和16,则此菱形的边长是( )
| A. | 10 | B. | 8 | C. | 6 | D. | 5 |
10.从$\sqrt{2}$,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
1.24的素因数是( )
| A. | 1,2,3,4,6,8,12,24 | B. | 2,3 | ||
| C. | 1,2,3 | D. | 2,2,2,3 |
 如图,在?ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为30°.
如图,在?ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为30°.