题目内容
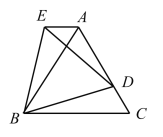
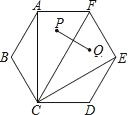
【题目】如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
A. 1 B. 2 C. 2![]() ﹣2 D. 4﹣2
﹣2 D. 4﹣2![]()
【答案】C
【解析】
先判断出PQ⊥CF,再求出AC=2![]() ,AF=2,CF=2AF=4,利用△ACF的面积的两种算法即可求出PG,然后计算出PQ即可.
,AF=2,CF=2AF=4,利用△ACF的面积的两种算法即可求出PG,然后计算出PQ即可.
解:如图,连接PF,QF,PC,QC
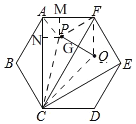
∵P、Q两点分别为△ACF、△CEF的内心,
∴PF是∠AFC的角平分线,FQ是∠CFE的角平分线,
∴∠PFC=![]() ∠AFC=30°,∠QFC=
∠AFC=30°,∠QFC=![]() ∠CFE=30°,
∠CFE=30°,
∴∠PFC=∠QFC=30°,
同理,∠PCF=∠QCF
∴PQ⊥CF,
∴△PQF是等边三角形,
∴PQ=2PG;
易得△ACF≌△ECF,且内角是30,60,90的三角形,
∴AC=2![]() ,AF=2,CF=2AF=4,
,AF=2,CF=2AF=4,
∴S△ACF=![]() AF×AC=
AF×AC=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
过点P作PM⊥AF,PN⊥AC,PQ交CF于G,
∵点P是△ACF的内心,
∴PM=PN=PG,
∴S△ACF=S△PAF+S△PAC+S△PCF
=![]() AF×PM+
AF×PM+![]() AC×PN+
AC×PN+![]() CF×PG
CF×PG
=![]() ×2×PG+
×2×PG+![]() ×2
×2![]() ×PG+
×PG+![]() ×4×PG
×4×PG
=(1+![]() +2)PG
+2)PG
=(3+![]() )PG
)PG
=2![]() ,
,
∴PG=![]() =
=![]() ,
,
∴PQ=2PG=2(![]() )=2
)=2![]() -2.
-2.
故选C.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目