题目内容
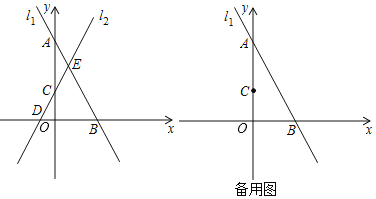
【题目】如图，已知直线l1：y1＝x+b经过点A（﹣5，0），交y轴于点B，直线l2：y2＝﹣2x﹣4与直线l1：y1＝x+b交于点C，交y轴于点D．
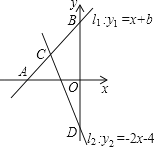
（1）求b的值；
（2）求△BCD的面积；
（3）当0≤y2＜y1时，则x的取值范围是 ．（直接写出结果）
【答案】（1）b=5；（2）
；（3）﹣3＜x≤﹣2
【解析】
（1）把点A的坐标代入直线l1：y1=x+b，列出方程并解答；
（2）利用两直线相交求得点C的坐标，由直线l2、l1求得点B、D的坐标，根据三角形的面积公式解答；
（3）结合图形直接得到答案．
（1）把A（﹣5，0）代入y1=x+b，得﹣5+b=0
解得b=5；
（2）由（1）知，直线l1：y1=x+5，且B（0，5）．
根题意知，
．
解得
，即C（﹣3，2）．
又由y2=﹣2x﹣4知，D（0，﹣4）．
所以 BD=9．
所以S△BCD=
BD|xC|=
=；
（3）由（2）知，C（﹣3，2）．
当y=0时，﹣2x﹣4=0，此时x=﹣2．
所以由图象知，当0≤y2＜y1时，则x的取值范围是﹣3＜x≤﹣2．
故答案是：﹣3＜x≤﹣2．
练习册系列答案
相关题目
