ЬтФПФкШн
ЁОЬтФПЁПЪмЁАаТЙкЁБвпЧщЕФгАЯьЃЌФГЯњЪлЩЬдкЭјЩЯЯњЪл![]() ЁЂ
ЁЂ![]() СНжжаЭКХЕФЁАЪжаДАхЁБЃЌЛёРћЦФЗсЃЎвбжЊ
СНжжаЭКХЕФЁАЪжаДАхЁБЃЌЛёРћЦФЗсЃЎвбжЊ![]() аЭЃЌ
аЭЃЌ![]() аЭЪжаДАхНјМлЁЂЪлМлКЭУПШеЯњСПШчБэИёЫљЪОЃК
аЭЪжаДАхНјМлЁЂЪлМлКЭУПШеЯњСПШчБэИёЫљЪОЃК
НјМлЃЈдЊ/ИіЃЉ | ЪлМлЃЈдЊ/ИіЃЉ | ЯњСПЃЈИі/ШеЃЉ | |
|
|
|
|
|
|
|
|
ИљОнЪаГЁааЧщЃЌИУЯњЪлЩЬЖд![]() аЭЪжаДАхНЕМлЯњЪлЃЌЭЌЪБЖд
аЭЪжаДАхНЕМлЯњЪлЃЌЭЌЪБЖд![]() аЭЪжаДАхЬсИпЪлМлЃЌДЫЪБЗЂЯж
аЭЪжаДАхЬсИпЪлМлЃЌДЫЪБЗЂЯж![]() аЭЪжаДАхУПНЕЕЭ
аЭЪжаДАхУПНЕЕЭ![]() дЊОЭПЩЖрТє
дЊОЭПЩЖрТє![]() ИіЃЌ
ИіЃЌ![]() аЭЪжаДАхУПЬсИп
аЭЪжаДАхУПЬсИп![]() дЊОЭЩйТє
дЊОЭЩйТє![]() ИіЃЌвЊБЃГжУПЬьЯњЪлзмСПВЛБфЃЌЩшЦфжа
ИіЃЌвЊБЃГжУПЬьЯњЪлзмСПВЛБфЃЌЩшЦфжа![]() аЭЪжаДАхУПЬьЖрЯњЪл
аЭЪжаДАхУПЬьЖрЯњЪл![]() ИіЃЌУПЬьзмЛёРћЕФРћШѓЮЊ
ИіЃЌУПЬьзмЛёРћЕФРћШѓЮЊ![]() дЊ
дЊ
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНВЂаДГі
жЎМфЕФКЏЪ§ЙиЯЕЪНВЂаДГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉвЊЪЙУПЬьЕФРћШѓВЛЕЭгк![]() дЊЃЌжБНгаДГі
дЊЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉИУЯњЪлЩЬОіЖЈУПЯњЪлвЛИі![]() аЭЪжаДАхЃЌОЭОш
аЭЪжаДАхЃЌОЭОш![]() дЊИј
дЊИј![]() вђЁАаТЙквпЧщЁБгАЯьЕФРЇФбМвЭЅЃЌЕБ
вђЁАаТЙквпЧщЁБгАЯьЕФРЇФбМвЭЅЃЌЕБ![]() ЪБЃЌУПЬьЕФзюДѓРћШѓЮЊ
ЪБЃЌУПЬьЕФзюДѓРћШѓЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ
ЃЈ![]() ЃЉЃЌЧвxЮЊећЪ§ЃЛЃЈ2ЃЉ
ЃЉЃЌЧвxЮЊећЪ§ЃЛЃЈ2ЃЉ![]() ЃЌЧвxЮЊећЪ§ЃЛЃЈ3ЃЉ
ЃЌЧвxЮЊећЪ§ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЩш![]() аЭЪжаДАхУПЬьЖрЯњЪл
аЭЪжаДАхУПЬьЖрЯњЪл![]() ИіЃЌдђBаЭЪжаДАхУПЬьЩйЯњЪл
ИіЃЌдђBаЭЪжаДАхУПЬьЩйЯњЪл![]() ИіЃЌИљОнзмЛёРћЕФРћШѓ
ИіЃЌИљОнзмЛёРћЕФРћШѓ![]() ЕШгкЯњЪлAаЭЪжаДАхЫљЛёРћШѓМгЩЯЯњЪлBаЭЪжаДАхЫљЛёРћШѓЃЌИљОнУПМўЯњЪлЕФРћШѓЃЌУПШеЕФЯњСПЖМЮЊЗЧИКЪ§Чв
ЕШгкЯњЪлAаЭЪжаДАхЫљЛёРћШѓМгЩЯЯњЪлBаЭЪжаДАхЫљЛёРћШѓЃЌИљОнУПМўЯњЪлЕФРћШѓЃЌУПШеЕФЯњСПЖМЮЊЗЧИКЪ§Чв![]() ЮЊЗЧИКећЪ§ЧѓГіxЕФШЁжЕЗЖЮЇЃЛ
ЮЊЗЧИКећЪ§ЧѓГіxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉНсКЯЃЈ1ЃЉНЋзмРћШѓКЏЪ§НјааХфЗНЃЌЧѓГіЕБ![]() ЪБЕФxжЕЃЌНсКЯЭМЯѓЕУЕНУПЬьЕФРћШѓВЛЕЭгк
ЪБЕФxжЕЃЌНсКЯЭМЯѓЕУЕНУПЬьЕФРћШѓВЛЕЭгк![]() дЊЪБЕФxЕФШЁжЕЗЖЮЇЃЌНјЖјЧѓНтЃЛ
дЊЪБЕФxЕФШЁжЕЗЖЮЇЃЌНјЖјЧѓНтЃЛ
ЃЈ3ЃЉЩшОшПюКѓУПЬьЕФРћШѓЮЊ![]() дЊЃЌдђ
дЊЃЌдђ![]() ЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНјааЧѓНтЃЎ
ЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНјааЧѓНтЃЎ
НтЃКЃЈ1ЃЉ ![]() ЃЌ
ЃЌ
ЛЏМђЕУЃЌ![]() ЃЌ
ЃЌ
гЩЬтвтжЊЃЌ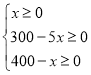 ЃЌ
ЃЌ
НтЕУЃЌ![]() ЃЌ
ЃЌ
ЙЪ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() Чв
Чв![]() ЮЊећЪ§ЃЛ
ЮЊећЪ§ЃЛ
ЃЈ2ЃЉ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЌ
ЃЌ
РэгЩШчЯТЃК![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() Лђ
Лђ![]() ЃЌ
ЃЌ
вЊЪЙ![]() ЃЌгЩЭМЯѓжЊЃЌ
ЃЌгЩЭМЯѓжЊЃЌ![]() ЃЛ
ЃЛ
![]() ЃЌ
ЃЌ
![]() ЃЌЧв
ЃЌЧв![]() ЮЊећЪ§ЃЛ
ЮЊећЪ§ЃЛ
ЃЈ3ЃЉЩшОшПюКѓУПЬьЕФРћШѓЮЊ![]() дЊЃЌ
дЊЃЌ
дђ![]() ЃЌ
ЃЌ
ЖдГЦжсЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ХзЮяЯпПЊПкЯђЯТЃЌЕБ
ХзЮяЯпПЊПкЯђЯТЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃЌ
ЕФдіДѓЖјдіДѓЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() зюДѓЃЌ
зюДѓЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃЌ![]() ЃЎ
ЃЎ

ЁОЬтФПЁПаЁЭѕЕчзгВњЦЗзЈЙёвд20дЊ/ИБЕФМлИёХњЗЂСЫФГаТПюЖњЛњЃЌдкЪдЯњЕФ60ЬьФкећРэГіСЫЯњЪлЪ§ОнШчЯТ
ЯњЪлЪ§Он(ЕкxЬь) | ЪлМл(дЊ) | ШеЯњЪлСП(ИБ) |
1ЁмxЃМ35 | x+30 | 100Љ2x |
35ЁмxЁм60 | 70 | 100Љ2x |
(1)ШєЪдЯњНзЖЮУПЬьЕФРћШѓЮЊWдЊЃЌЧѓГіWгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЧыЮЪдкЪдЯњНзЖЮЕФФФвЛЬьЯњЪлРћШѓWПЩвдДяЕНзюДѓжЕЃПзюДѓжЕЮЊЖрЩйЃП