题目内容
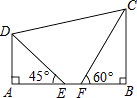
【题目】在等腰直角三角形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是斜边
是斜边![]() 的中点,连接
的中点,连接![]() .
.
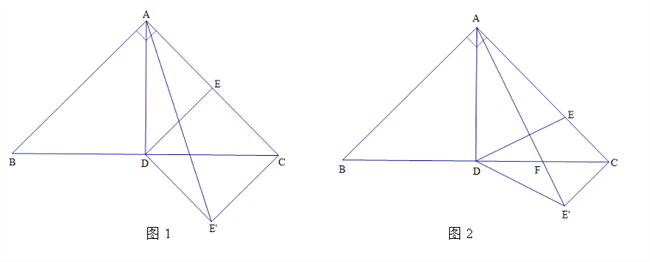
(1)如图1, ![]() 是
是![]() 的中点,连接
的中点,连接![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)如图2,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() 的值为
的值为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)在等腰直角三角形中先求出AC的长,再在Rt△ACE′中,理由勾股定理求出AE′的长即可;(2)B作AE’的垂线交AD于点G,交AC于点H,由角角边可证△ABH≌△CAE′,所以AH=HE=CE,进而D是BC中点,由中位线定理得DE//BH ,再由角角边得△ABG≌△CAF,得到AG=CF进而DF=CF.
试题解析:(1)∵![]() ,
, ![]() ,D是斜边
,D是斜边![]() 的中点,
的中点,
∴![]() ,∠ACD=45°,
,∠ACD=45°,
在RtADC中:AC=AD.sin45°=![]()
∵E是AC的中点
∴CE=![]() AC=
AC=![]()
∵将△CDE沿CD翻折到△CDE′
∴CE′=CE=![]() , ∠ACE′=90°,由勾股定理得:
, ∠ACE′=90°,由勾股定理得:
AE′=![]()
过B作AE’的垂线交AD于点G,交AC于点H
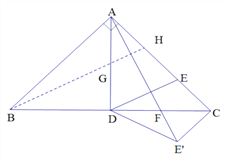
∵∠ABH+∠BAF=90°,∠CAF+∠BAF=90°
∴∠ABH=∠CAF
又∵AB=AC,∠BAH=∠ACE’=90°
∴△ABH≌△CAE′
∴AH=CE′=CE
∵![]()
∴AH=HE=CE
∵D是BC中点
∴DE//BH
∴G是AD中点
在ABG和CAF中:AB=AC,∠BAD=∠ACD=45°,∠ABH=∠CAF
∴△ABG≌△CAF
∴AG=CF
∵AG=![]() AD
AD
∴CF=![]() AD=
AD=![]() CD
CD
∴DF=CF

练习册系列答案
相关题目
【题目】用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出了如下表格:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
y=ax2+bx+c(a≠0) | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
那么当该二次函数值y > 0时,x的取值范围是_________.