题目内容
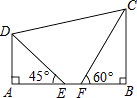
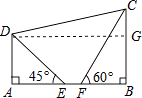
【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
. 
(1)BC= .
(2)求点D到BC的距离.
(3)求DC的长.
【答案】
(1)3
(2)解:过点D作DG⊥BC于点G,
∵AD∥BC,AB⊥BC,
∴DG=AB,DA⊥AB,
∵FC=2 ![]() ,∠BFC=60°,
,∠BFC=60°,
∴BF=FCcos60°= ![]() ,
,
∴DC=AB=AE+EF+BF=2+2﹣ ![]() +
+ ![]() =4
=4
(3)解:∵DA⊥AB,∠AED=45°,
∴AD=AE=2,
∵DG⊥BC,AB⊥BC,
∴DG∥AB,
∵AD∥BC,
∴四边形ABGD是平行四边形,
∴BG=AD=2,
∴CG=BC﹣BG=3﹣2=1,
∴在Rt△DCG中,CD= ![]() =
= ![]() .
.
【解析】解:(1)∵AB⊥BC,
∴∠B=90°,
∵FC=2 ![]() ,∠BFC=60°,
,∠BFC=60°,
∴BC=FCsin60°=2 ![]() ×
× ![]() =3;
=3;
故答案为:3;
(1)由AB⊥BC,FC=2 ![]() °,∠BFC=60°,直接利用三角函数的知识求解即可求得答案;(2)首先过点D作DG⊥BC于点G,由AD∥BC,AB⊥BC,可得DG=AB,继而求得答案;(3)首先可得四边形ABGD是平行四边形,即可求得CG的长,然后由勾股定理求得答案.
°,∠BFC=60°,直接利用三角函数的知识求解即可求得答案;(2)首先过点D作DG⊥BC于点G,由AD∥BC,AB⊥BC,可得DG=AB,继而求得答案;(3)首先可得四边形ABGD是平行四边形,即可求得CG的长,然后由勾股定理求得答案.

练习册系列答案
相关题目