Question

13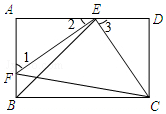．如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．
（1）求证：△AEF≌△DCE；
（2）若CD=1，求BE的长．

Answer 1

分析 （1）根据矩形的性质和已知条件可证明△AEF≌△DCE；
（2）由（1）可知AE=DC，在Rt△ABE中由勾股定理可求得BE的长．

解答 （1）证明：在矩形ABCD中，∠A=∠D=90°，
∴∠1+∠2=90°，
∵EF⊥EC，
∴∠FEC=90°，
∴∠2+∠3=90°，
∴∠1=∠3，
在△AEF和△DCE中，
$\left\{\begin{array}{l}{∠A=∠D}\\{∠1=∠3}\\{EF=EC}\end{array}\right.$，
∴△AEF≌△DCE（AAS）；

（2）解：由（1）知△AEF≌△DCE，
∴AE=DC=1，
在矩形ABCD中，AB=CD=1，
在R△ABE中，AB²+AE²=BE²，即1²+1²=BE²，
∴BE=$\sqrt{2}$．

点评 本题主要考查矩形的性质和全等三角形的判定和性质，在（1）中证得三角形全等是解题的关键，在（2）中注意勾股定理的应用．