题目内容
(1)如图1,点E为?ABCD的边AD上一点,点P为CD中点,连结EP并延长与BC的延长线交于点F.
求证:DE=CF.
(2)如图2,在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,求该高楼的高度.

求证:DE=CF.
(2)如图2,在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,求该高楼的高度.

考点:解直角三角形的应用-仰角俯角问题,全等三角形的判定与性质,平行四边形的性质
专题:
分析:(1)根据平行四边形的性质可得DE∥CF,然后可得∠DEP=∠F,然后根据点P为CD中点可得PC=PD,最后利用AAS可证明△EDP≌△FCP,继而可得DE=CF;
(2)设楼高为h,分别在Rt△ABD和Rt△ABC中,表示出BD和BC,根据CD=60米,列方程求出h的值.
(2)设楼高为h,分别在Rt△ABD和Rt△ABC中,表示出BD和BC,根据CD=60米,列方程求出h的值.
解答:解:(1)∵四边形ABCD为平行四边形,
∴DE∥CF,
∴∠DEP=∠F,
∵点P为CD中点,
∴PC=PD,
在△EDP和△FCP中,
,
∴△EDP≌△FCP(AAS),
∴DE=CF;
(2)设楼高为h,
在Rt△ABD中,
∵∠ADB=30°,
∴BD=
h,
在Rt△ABC中,
∵∠ABC=45°,
∴BC=h,
∵BD-BC=60,
∴
h-h=60,
解得:h=30(
+1).
答:该高楼的高度为30(
+1)米.
∴DE∥CF,
∴∠DEP=∠F,
∵点P为CD中点,
∴PC=PD,
在△EDP和△FCP中,
|
∴△EDP≌△FCP(AAS),
∴DE=CF;
(2)设楼高为h,
在Rt△ABD中,
∵∠ADB=30°,
∴BD=
| 3 |
在Rt△ABC中,
∵∠ABC=45°,
∴BC=h,
∵BD-BC=60,
∴
| 3 |
解得:h=30(
| 3 |
答:该高楼的高度为30(
| 3 |
点评:本题考查了全等三角形的判定和性质以及解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
相关题目
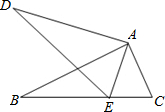 如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.
如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.