题目内容
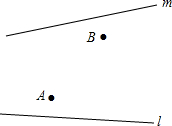如图，在旷野上，一个人骑着马从A到B，半路上他必须先到河岸l的P点去让马饮水，然后再让马到河岸m的Q点再次饮水，最后到达B点，他应该如何选择饮马地点P、Q，才能使所走路程AP+PQ+QB为最短（假设河岸l、m为直线）．考点：轴对称-最短路线问题
专题：
分析：作出点A关于l的对称点A′，点B关于m的对称点B′，连接A′B′，交于l，m于点P，点Q，则AP，PQ，QB是他走的最短路线．
解答：
解：如图，分别作A点关于直线l的对称点A′、B点关于直线m的对称点B′
连接A′B′，分别交l于点P，交m于点Q，
连接AP、BQ，
所以路程AP+PQ+BQ最短．
解：如图，分别作A点关于直线l的对称点A′、B点关于直线m的对称点B′连接A′B′，分别交l于点P，交m于点Q，
连接AP、BQ，
所以路程AP+PQ+BQ最短．
点评：本题考查了轴对称的性质-最短路线问题，利用两点之间线段最短的性质求解是解本题的关键．
练习册系列答案
相关题目
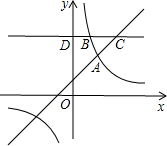如图，一次函数y=kx+1（k≠0）与反比例函数y=
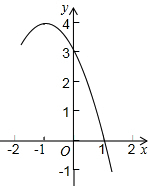已知抛物线y=-x2+bx-c的部分图象如图所示．
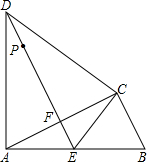如图，△ABC中，∠ACB=90°，以AC为一边在△ABC作等边三角形ACD，过点D作DE⊥AC，垂足为F，DE与AB相交于点E，连接CE．
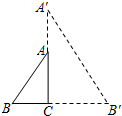如图，在Rt△ABC中，∠ACB=90°，AB=5，cosB=