题目内容
如图，在Rt△DBC中，∠B=90°，∠D=30°，点A在边DB上，AC=12，cos∠ACB=| 2 | 3 |
分析：求出BC，求出DC=2BC，代入求出即可，根据勾股定理求出DB，根据三角形的面积公式求出即可．
解答：解：∵cos∠ACB=
=
，AC=12，
∴BC=8，
∵∠B=90°，∠D=30°，
∴DC=2BC=16，
由勾股定理得：DB=
=8
，
∴△DBC的面积是
×8×8
=32
．
| 2 |
| 3 |
| BC |
| AC |
∴BC=8，
∵∠B=90°，∠D=30°，
∴DC=2BC=16，
由勾股定理得：DB=
| 162-82 |
| 3 |
∴△DBC的面积是
| 1 |
| 2 |
| 3 |
| 3 |
点评：本题考查了锐角三角函数的定义，解直角三角形，勾股定理，三角形的面积等知识点的应用．
练习册系列答案
相关题目
22、已知：如图，在Rt△ABC中，∠C=90°，D是AC上一点，DE⊥AB于E，且DE=DC．
如图，在Rt△ABC中，∠C=90°，BC=8
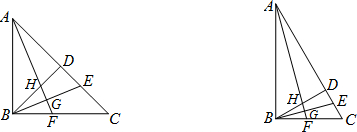
如图，在Rt△DBC中，∠B=90°，∠D=30°，点A在边DB上，AC=12，cos∠ACB=
．求DC长及△DBC的面积．