题目内容
(2012•昌平区二模)如图,在Rt△ABC中,∠ABC=90°,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.
(1)若∠BAC=45°,求证:①AF平分∠BAC;②FC=2HD.
(2)若∠BAC=30°,请直接写出FC与HD的等量关系.
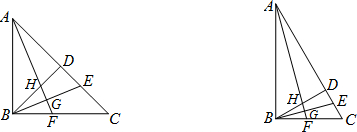
(1)若∠BAC=45°,求证:①AF平分∠BAC;②FC=2HD.
(2)若∠BAC=30°,请直接写出FC与HD的等量关系.
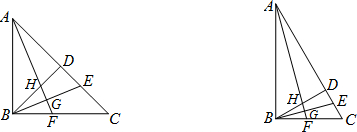
分析:(1)①首先证明∠HBG=∠HAD,再证明∠GBF=∠BAF,再根据∠GBF=∠HBG可得∠HAD=∠BAF,进而得到结论;
②过点D作KD∥FC交AF于K,然后可以证出
=
=
进而得到FC=2KD,再证明∠DKH=∠DHK得到KD=HD,进而得到FC=2HD;
(2)与(1)中的②证明方法类似,首先证明
=
,再根据MD∥FC可得
=
=
,然后再证明MD=HD,进而得到结论.
②过点D作KD∥FC交AF于K,然后可以证出
| KD |
| FC |
| AD |
| AC |
| 1 |
| 2 |
(2)与(1)中的②证明方法类似,首先证明
| AD |
| AC |
| 3 |
| 4 |
| MD |
| FC |
| AD |
| AC |
| 3 |
| 4 |
解答: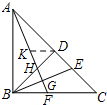 解:(1)①∵BD⊥AC,AF⊥BE,
解:(1)①∵BD⊥AC,AF⊥BE,
∴∠ADH=∠HGB=90°.
∵∠BHG=∠AHD,
∴∠HBG=∠HAD.
∵∠ABC=∠FGB=90°,
∴∠BAF+∠AFB=90°,
∠GBF+∠AFB=90°.
∴∠GBF=∠BAF.
∵BE平分∠DBC,
∴∠GBF=∠HBG.
∴∠HAD=∠BAF.
即 AF平分∠BAC.
②∵在Rt△ABC中,∠ABC=90°,∠BAC=45°,
∴∠C=∠BAC=45°,
∴AB=BC.
∵BD⊥AC,
∴AD=DC=
AC.
过点D作KD∥FC交AF于K,
∴
=
=
.
∴FC=2KD,
∵BE平分∠DBC,BE⊥AF,
∴∠DBE=∠EBF,∠HGB=∠FGB=90°.
∴∠BFH=∠BHF.
∴∠BHF=∠DHK.
∴∠BFH=∠DHK.
∵KD∥BC,
∴∠DKH=∠BFH.
∴∠DKH=∠DHK.
∴KD=HD.
∴FC=2HD.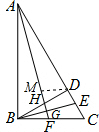
(2)过点D作MD∥FC交AF于M,
∵在Rt△ABC中,∠ABC=90°,∠BAC=30°,
∴
=
,
=
,
∴
=
,
∵MD∥FC,
∴
=
=
,
∵BE平分∠DBC,BE⊥AF,
∴∠DBE=∠EBF,∠HGB=∠FGB=90°.
∴∠BFH=∠BHF.
∵∠BHF=∠DHM.
∴∠BFH=∠DHM.
∵MD∥BC,
∴∠DMH=∠BFH.
∴∠DMH=∠DHM.
∴MD=HD.
∴
=
.
∴FC=
HD.
 解:(1)①∵BD⊥AC,AF⊥BE,
解:(1)①∵BD⊥AC,AF⊥BE,∴∠ADH=∠HGB=90°.
∵∠BHG=∠AHD,
∴∠HBG=∠HAD.
∵∠ABC=∠FGB=90°,
∴∠BAF+∠AFB=90°,
∠GBF+∠AFB=90°.
∴∠GBF=∠BAF.
∵BE平分∠DBC,
∴∠GBF=∠HBG.
∴∠HAD=∠BAF.
即 AF平分∠BAC.
②∵在Rt△ABC中,∠ABC=90°,∠BAC=45°,
∴∠C=∠BAC=45°,
∴AB=BC.
∵BD⊥AC,
∴AD=DC=
| 1 |
| 2 |
过点D作KD∥FC交AF于K,
∴
| KD |
| FC |
| AD |
| AC |
| 1 |
| 2 |
∴FC=2KD,
∵BE平分∠DBC,BE⊥AF,
∴∠DBE=∠EBF,∠HGB=∠FGB=90°.
∴∠BFH=∠BHF.
∴∠BHF=∠DHK.
∴∠BFH=∠DHK.
∵KD∥BC,
∴∠DKH=∠BFH.
∴∠DKH=∠DHK.
∴KD=HD.
∴FC=2HD.

(2)过点D作MD∥FC交AF于M,
∵在Rt△ABC中,∠ABC=90°,∠BAC=30°,
∴
| AD |
| AB |
| ||
| 2 |
| AB |
| AC |
| ||
| 2 |
∴
| AD |
| AC |
| 3 |
| 4 |
∵MD∥FC,
∴
| MD |
| FC |
| AD |
| AC |
| 3 |
| 4 |
∵BE平分∠DBC,BE⊥AF,
∴∠DBE=∠EBF,∠HGB=∠FGB=90°.
∴∠BFH=∠BHF.
∵∠BHF=∠DHM.
∴∠BFH=∠DHM.
∵MD∥BC,
∴∠DMH=∠BFH.
∴∠DMH=∠DHM.
∴MD=HD.
∴
| HD |
| FC |
| 3 |
| 4 |
∴FC=
| 4 |
| 3 |
点评:此题主要考查了平行线分线段成比例定理,关键是证明KD=HD和MD=HD.此题综合性较强,找准角之间的相等关系是解决此题的难点.

练习册系列答案
相关题目
 (2012•昌平区二模)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABC=70°,则∠BDC的度数为( )
(2012•昌平区二模)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABC=70°,则∠BDC的度数为( )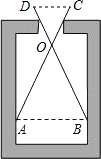 (2012•昌平区二模)如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10,则零件的内孔直径AB长为( )
(2012•昌平区二模)如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10,则零件的内孔直径AB长为( ) (2012•昌平区二模)如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是
(2012•昌平区二模)如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是