题目内容
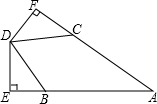 已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.考点:全等三角形的判定与性质
专题:常规题型
分析:连接AD,易证△ACD≌△ABD,根据全等三角形对应角相等的性质可得∠EAD=∠FAD,再根据∠AED=∠AFD,AD=AD,即可证明△ADE≌△ADF,根据全等三角形对应边相等的性质可得DE=DF.
解答:证明:
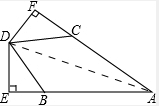
连接AD,在△ACD和△ABD中,
,
∴ACD≌△ABD(SSS),
∵DE⊥AE,DF⊥AF,
∴∠AED=∠AFD=90°,
∴在△ADE和△ADF中,
,
∴△ADE≌△ADF,
∴DE=DF.

连接AD,在△ACD和△ABD中,
|
∴ACD≌△ABD(SSS),
∵DE⊥AE,DF⊥AF,
∴∠AED=∠AFD=90°,
∴在△ADE和△ADF中,
|
∴△ADE≌△ADF,
∴DE=DF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质.

练习册系列答案
相关题目
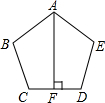 已知,如图,AB=AE,∠BAF=∠EAF,AF⊥CD,且F为CD中点,试说明:BC=ED.
已知,如图,AB=AE,∠BAF=∠EAF,AF⊥CD,且F为CD中点,试说明:BC=ED. 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE=90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE=90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由.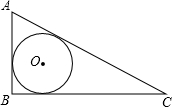 如图,在Rt△ABC中,内切圆⊙O分别与AB、AC、BC相切,且AB=5,AC=13,求内切圆的半径.
如图,在Rt△ABC中,内切圆⊙O分别与AB、AC、BC相切,且AB=5,AC=13,求内切圆的半径.
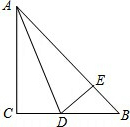 如图所示,在等腰直角△ABC中∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E.若AB=10cm,则△DEB的周长为
如图所示,在等腰直角△ABC中∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E.若AB=10cm,则△DEB的周长为