题目内容
 如图,⊙O的直径为10,点A、B、C在⊙O上,∠CAB的平分线AD交⊙O于点D.若∠CAB=60°,则BD的长为
如图,⊙O的直径为10,点A、B、C在⊙O上,∠CAB的平分线AD交⊙O于点D.若∠CAB=60°,则BD的长为考点:圆周角定理,等边三角形的判定与性质
专题:计算题
分析:连接OB、OD,如图,先根据角平分线的定义得到∠BAD=
∠CAB=30°,再根据圆周角定理得到∠BOD=2∠BAD=60°,于是可判断△OBD为等边三角形,然后根据等边三角形的性质求解.
| 1 |
| 2 |
解答:解 :连接OB、OD,如图,
:连接OB、OD,如图,
∵AD平分∠CAB,
∴∠BAD=
∠CAB=
×60°=30°,
∴∠BOD=2∠BAD=60°,
而OB=OD,
∴△OBD为等边三角形,
∴BD=OB=
×10=5.
故答案为5.
 :连接OB、OD,如图,
:连接OB、OD,如图,∵AD平分∠CAB,
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOD=2∠BAD=60°,
而OB=OD,
∴△OBD为等边三角形,
∴BD=OB=
| 1 |
| 2 |
故答案为5.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等边三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图图象可能是关于x的一次函数y=k(x-1)的图象的是( )
A、 |
B、 |
C、 |
D、 |
函数y=2x-5的图象一定过( )
| A、(-2,1) |
| B、(2,-1) |
| C、(-1,2) |
| D、(1,-2) |
下列图形中,是圆周角的是( )
A、 |
B、 |
C、 |
D、 |
 如图,正比例函数与一次函数交于点A(3,4),且一次函数与x轴交于点C,与y轴交于点B,
如图,正比例函数与一次函数交于点A(3,4),且一次函数与x轴交于点C,与y轴交于点B,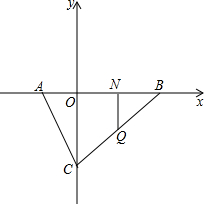 如图,在平面直角坐标系中,已知A(-1,0),B(3,0),C(0,-3),在线段BC上取一点Q(不与点B、点C重合),作QN⊥x轴于N,设线段QN长为t.
如图,在平面直角坐标系中,已知A(-1,0),B(3,0),C(0,-3),在线段BC上取一点Q(不与点B、点C重合),作QN⊥x轴于N,设线段QN长为t.