题目内容
20. 已知点D为等腰直角三角形ABC的斜边AB上一点,连接CD,DE⊥CD,DE=CD,连接AE,CE,求证:AE∥BC.
已知点D为等腰直角三角形ABC的斜边AB上一点,连接CD,DE⊥CD,DE=CD,连接AE,CE,求证:AE∥BC.
分析 利用相似三角形的判定方法得出△AFC∽△EFD,进而得出△AFE∽△CFD,求出∠EAF+∠CAD=90°,进而利用平行线的判定得出即可.
解答  证明:∵△ACB为等腰直角三角形,DE⊥CD,DE=CD,
证明:∵△ACB为等腰直角三角形,DE⊥CD,DE=CD,
∴∠CAB=∠CED=45°,
又∵∠AFC=∠EFD,
∴△AFC∽△EFD,
∴$\frac{AE}{EF}=\frac{FC}{FD}$,
∴$\frac{AF}{FC}=\frac{EF}{FD}$,
又∵∠AFE=∠DFC,
∴△AFE∽△CFD,
∴∠EAF=∠DCF=45°,
∴∠EAF+∠CAD=90°,
∵∠ACB=90°,
∴∠EAC+∠ACB=180°,
∴AE∥BC.
点评 此题主要考查了相似三角形的判定与性质,熟练掌握相似三角形的判定方法得出△AFE∽△CFD是解题关键.

练习册系列答案
相关题目
12.一个不透明的布袋里装有7个只有颜色不同的球,其中4个红球,3个白球,从布袋中随机摸出一个球,摸出的球是红球的概率是( )
| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
10. 如图,已知△ABD≌△ACE,则下列说法中不正确的是( )
如图,已知△ABD≌△ACE,则下列说法中不正确的是( )
 如图,已知△ABD≌△ACE,则下列说法中不正确的是( )
如图,已知△ABD≌△ACE,则下列说法中不正确的是( )| A. | AB=AC | B. | ∠B=∠C | C. | BE=CD | D. | ∠BAE=∠ADC |
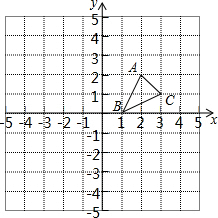 如图,平面直角坐标系中每个小方格均是边长为1个单位的正方形,△ABC的顶点均在格点上,点B的坐标为(1,0),按下列要求作图.
如图,平面直角坐标系中每个小方格均是边长为1个单位的正方形,△ABC的顶点均在格点上,点B的坐标为(1,0),按下列要求作图.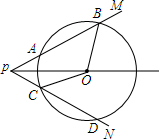 如图,点O是∠MPN的平分线上一点,以点O为圆心的圆和PM,PN分别相交于A,B,C,D四点,连接OB,OC.
如图,点O是∠MPN的平分线上一点,以点O为圆心的圆和PM,PN分别相交于A,B,C,D四点,连接OB,OC.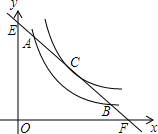 如图,直线y=-x+m与y=$\frac{4}{x}$只有唯一公共点C,与y=$\frac{k}{x}$交于A、B,且AC=$\frac{3}{2}$$\sqrt{2}$,求k.
如图,直线y=-x+m与y=$\frac{4}{x}$只有唯一公共点C,与y=$\frac{k}{x}$交于A、B,且AC=$\frac{3}{2}$$\sqrt{2}$,求k.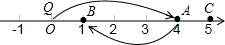 如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.
如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.