题目内容
 如图,在平面直角坐标系中,OBCD是正方形,B点的坐标为(2,1),则C点的坐标为
如图,在平面直角坐标系中,OBCD是正方形,B点的坐标为(2,1),则C点的坐标为考点:全等三角形的判定与性质,坐标与图形性质,正方形的性质
专题:
分析:过点B、C分别作x轴的垂线,分别交于点E、F,CF交0B于点G.分别得出△OGF∽△OBE,△OGF∽△CGB,利用OE:BE=2:1,和正方形的边长解决问题即可.
解答: 解:如图,
解:如图,
过点B、C分别作x轴的垂线,分别交于点E、F,CF交0B于点G;BH⊥CF于点F.
∵B点的坐标为(2,1),
∴OB=
=
,
∴正方形的边长为
,
∵GF⊥OE,BE⊥OE,
∴GF∥BE
∴△OGF∽△OBE,
∴
=
=2
∵∠GFO=∠CBG=90°,∠OGF=∠CGB
∴△OGF∽△CGB,
∴
=
=2
∴BG=
BC=
,
由勾股定理得GF=
,OF=1
在△GOF和△GBH中
∴△GOF≌△GBH(AAS)
∴GF=GH=
,
同理可以得出在△CHB中,
得出
=2,
由勾股定理得出CH=2,
∴CF=CH+HF=3,
则C点的坐标为(3,1).
故答案为:(1,3).
 解:如图,
解:如图,过点B、C分别作x轴的垂线,分别交于点E、F,CF交0B于点G;BH⊥CF于点F.
∵B点的坐标为(2,1),
∴OB=
| OE2+BE2 |
| 5 |
∴正方形的边长为
| 5 |
∵GF⊥OE,BE⊥OE,
∴GF∥BE
∴△OGF∽△OBE,
∴
| OF |
| FG |
| OE |
| BE |
∵∠GFO=∠CBG=90°,∠OGF=∠CGB
∴△OGF∽△CGB,
∴
| OF |
| FG |
| BG |
| BC |
∴BG=
| 1 |
| 2 |
| ||
| 2 |
由勾股定理得GF=
| 1 |
| 2 |
在△GOF和△GBH中
|
∴△GOF≌△GBH(AAS)
∴GF=GH=
| 1 |
| 2 |
同理可以得出在△CHB中,
得出
| CH |
| HB |
由勾股定理得出CH=2,
∴CF=CH+HF=3,
则C点的坐标为(3,1).
故答案为:(1,3).
点评:本题考查了正方形的性质,坐标与图形性质,作辅助线构造出直角三角形是解题的关键,要注意点C的横坐标是负数.

练习册系列答案
相关题目
某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机进校园”现象的看法,统计整理并制作了如下的统计图:
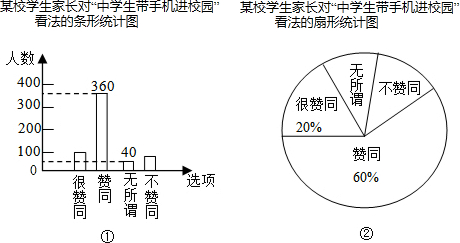
这次调查的家长总数为( )

这次调查的家长总数为( )
| A、240 | B、360 |
| C、600 | D、1800 |
 实数a、b、c在数轴上表示如图,则
实数a、b、c在数轴上表示如图,则