题目内容
20.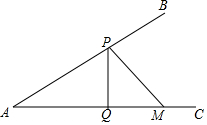 如图,∠BAC=30°,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为$\sqrt{3}$.
如图,∠BAC=30°,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为$\sqrt{3}$.
分析 本题作点M关于AB的对称点N,根据轴对称性找出点P的位置,如图,根据三角函数求出MN,∠N,再根据三角函数求出结论.
解答 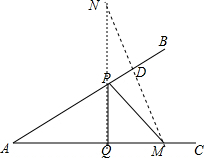 解:作点M关于AB的对称点N,过N作NQ⊥AC于Q交AB于P,
解:作点M关于AB的对称点N,过N作NQ⊥AC于Q交AB于P,
则NQ的长即为PM+PQ的最小值,
连接MN交AB于D,则MD⊥AB,DM=DN,
∵∠NPB=∠APQ,
∴∠N=∠BAC=30°,
∵∠BAC=30°,AM=2,
∴MD=$\frac{1}{2}$AM=1,
∴MN=2,
∴NQ=MN•cos∠N=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查含30°直角三角形的性质、轴对称--最短路线问题及三角函数,正确确定P点的位置是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.若x=-3,y=1,则代数式2x-3y+1的值为( )
| A. | -10 | B. | -8 | C. | 4 | D. | 10 |
8.下面四个几何体:

其中,俯视图是四边形的几何体个数是( )

其中,俯视图是四边形的几何体个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
则他们捐款金额的中位数和平均数分别是( )
| 金额/元 | 5 | 10 | 20 | 50 | 100 |
| 人数 | 4 | 16 | 15 | 9 | 6 |
| A. | 10,20.6 | B. | 20,20.6 | C. | 10,30.6 | D. | 20,30.6 |
2.一池塘中大约有鱼苗数为50 000尾,为了解池塘中鱼苗的长势,现需从中捞取一些鱼苗进行抽样调查,那么捞出鱼苗数最合适的是( )
| A. | 1尾 | B. | 50尾 | C. | 500尾 | D. | 1 000尾 |
6.某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.

根据以上信息解决下列问题:
(1)在统计表中,m=30,n=20,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是90°.
(3)若该校共有1120名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | m |
| E | 32≤x<40 | n |

根据以上信息解决下列问题:
(1)在统计表中,m=30,n=20,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是90°.
(3)若该校共有1120名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
 如图,E是?ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.
如图,E是?ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.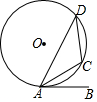 如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.
如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.