题目内容
9.如图1,在矩形ABCD中,AB<BC<2AB,点P、Q同时从点B出发,点P以每秒1个单位长度的速度沿B→A→D→C运动,点Q以每秒2个单位长度的速度沿B→C→D→A运动.当点P、Q相遇时,同时停止运动,设运动时间为t,△BPQ的面积为S,S关于t的函数图象如图2所示,(其中0<t≤4,4<t≤6,6<t≤m,m<t<n时,函数的解析式不同)(1)填空:BC=8,AB=6;
(2)求出S关于t的函数关系式,并写出t的取值范围.
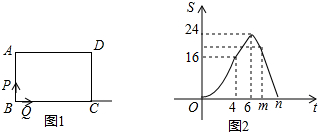
分析 (1)根据函数图象和在矩形ABCD中,AB<BC<2AB,点P、Q同时从点B出发,点P以每秒1个单位长度的速度沿B→A→D→C运动,点Q以每秒2个单位长度的速度沿B→C→D→A运动,可以得到BC和AB的长;
(2)根据函数图象和第(1)问中求得的BC、AB的长,可以求得各段的函数解析式.
解答 解:(1)由函数图象可知,
点Q从B到C运动的时间为4秒,
故BC=2×4=8,
点P从点B运动到点A用的时间是6秒,
故AB=1×6=6,
故答案为:8,6;
(2)由图象可得,
当0<t≤4时,$S=\frac{2t•t}{2}={t}^{2}$;
当4<t≤6时,$S=\frac{t•8}{2}=4t$;
∵AB=6,BC=8,
∴m=$\frac{8+6}{2}=7$,n=$\frac{8+8+6+6}{3}=\frac{28}{3}$,
当6<t≤7时,$S=6×8-\frac{(t-6)×6}{2}-\frac{8×(2t-8)}{2}-\frac{(6+8-t)(6+8-2t)}{2}$=-t2+10t,
当7<t<$\frac{28}{3}$时,S=$\frac{(8+6+8+6-2t-t)×6}{2}$=-9t+84,
即S=$\left\{\begin{array}{l}{{t}^{2}}&{0<t≤4}\\{4t}&{4<t≤6}\\{-{t}^{2}+10t}&{6≤t<7}\\{-9t+84}&{7<t<\frac{28}{3}}\end{array}\right.$.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
相关题目
19.已知反比例函数的图象经过点P(a,a),则这个函数的图象位于( )
| A. | 第一、三象限 | B. | 第二、三象限 | C. | 第二、四象限 | D. | 第三、四象限 |
17.在Rt△ABC中,∠C=90°,BC=4,AC=3,将△ABC绕着点B顺时针旋转后,点A落在射线BC上的点A′,点C落在点C′处,那么CC′的值为( )
| A. | 3 | B. | 4 | C. | $\frac{12}{5}$ | D. | $\frac{4}{5}$$\sqrt{10}$ |
14.我国最长的河流长江全长约为6300千米,数6300用科学记数法表示为( )
| A. | 0.63×104 | B. | 6.3×103 | C. | 63×102 | D. | 6.3×106 |
19.下列四个实数中最小的是( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1.4 |
 如图,一次函数y1=kx+b与反比例函数y2=$\frac{m}{x}$的图象相交于两点(-1,3)、(3,-1),则当y1<y2时,x的取值范围是-1<x<0或x>3.
如图,一次函数y1=kx+b与反比例函数y2=$\frac{m}{x}$的图象相交于两点(-1,3)、(3,-1),则当y1<y2时,x的取值范围是-1<x<0或x>3.