题目内容
18.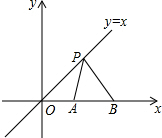 如图,点P是直线y=x上的动点,A(2,0),B(4,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{5}$.
如图,点P是直线y=x上的动点,A(2,0),B(4,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{5}$.
分析 首先作出点A关于y=x的对称点A′,从而得到PA=PA′,故此PA+PB=PA′+PB,由两点之间线段最短可知A′B即为所求.
解答 解:取点A′使OA′=OA,连接A′B.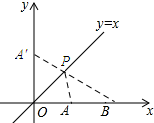
∴点A′的坐标为(0,2).
∴点A′与点A关于y=x对称.
∴PA′=PA.
∴PA+PB=PA′+PB.
由两点之间线段最短可知:当点A′、P、B在一条直线上时,PA+PB有最小值.
在Rt△A′OB中,A′B=$\sqrt{OA{′}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题主要考查的是最短线路问题,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.小华向果农买一竹篮的水果,含竹篮称得总重量为15斤,付水果的钱130元,若他再加买1斤的水果,需多付10元,则空竹篮的重量为( )
| A. | 1.5斤 | B. | 2斤 | C. | 2.5斤 | D. | 3斤 |
6.下列各组数中,数值相等的是( )
| A. | 23和32 | B. | -53和(-5)3 | C. | (-$\frac{2}{3}$)2和(-$\frac{3}{2}$)2 | D. | (-3)4和(-4)3 |
4.若|x|=|y|,那么x与y之间的关系是( )
| A. | 相等 | B. | 互为相反数 | ||
| C. | 相等或互为相反数 | D. | 无法判断 |