题目内容
5.已知-3x2+mx-6=0的一个根是1,求m及另一个根.分析 利用一元二次方程的根与系数的关系,两根的和是-m,两个根的积是2,即可求解.
解答 解:设方程的另一个解是a,则1×a=2,1+a=$\frac{m}{3}$,
解得:a=2,m=9,
即m的值是9,方程的另一根是2.
点评 本题考查了一元二次方程的根与系数的关系,正确理解根与系数的关系是关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
15.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (-3)2=6 | C. | (-a3)2=a6 | D. | a2+a3=a5 |
13.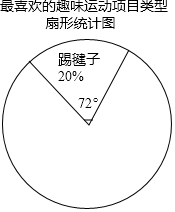 某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
(1)直接写出a=0.25,b=40;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
 某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
| 项目类型 | 频数 | 频率 |
| 跳长绳 | 25 | a |
| 踢毽子 | 20 | 0.2 |
| 背夹球 | b | 0.4 |
| 拔河 | 15 | 0.15 |
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
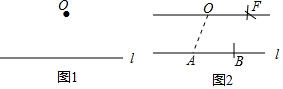 下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.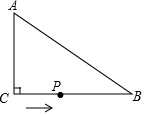 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.