题目内容
19．三角形的三边长为a，b，c，且满足（a+b）2=c2+2ab，则这个三角形是直角三角形．分析 先根据完全平方公式对已知等式进行化简，再根据勾股定理的逆定理进行判定．
解答 解：∵（a+b）2=c2+2ab，
∴a2+2ab+b2-c2=2ab，
∴a2+b2=c2，
∴三角形是直角三角形．
故答案为直角三角形．
点评 本题考查了勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．也考查了完全平方公式．
练习册系列答案
相关题目
、小明掷B立方体朝上的数字为
来确定点P（
），那么它们各掷一次所确定的点P落在已知抛物线
上的概率为（ ）
B. 
C. 
D. 
10．
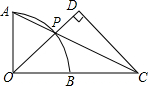如图，点O为弧AB所在圆的圆心，OA⊥OB，点P在弧AB上，AP的延长线与OB的延长线交于点C，过点C作CD⊥OP于D．若OB=BC=1，则PD的长为（ ）
如图，点O为弧AB所在圆的圆心，OA⊥OB，点P在弧AB上，AP的延长线与OB的延长线交于点C，过点C作CD⊥OP于D．若OB=BC=1，则PD的长为（ ）| A． | $\frac{2}{5}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
如图，一条船从灯塔C的南偏东42°的A处出发，向正北航行8海里到达B处，此时灯塔C在船的北偏西84°方向，则船距离灯塔C8海里．
11．
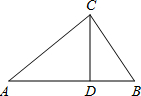如图，在Rt△ABC中，CD是斜边AB上的高，若BD=4，CD=6，则AD的长为（ ）
如图，在Rt△ABC中，CD是斜边AB上的高，若BD=4，CD=6，则AD的长为（ ）| A． | 8 | B． | 9 | C． | 10 | D． | 12 |
如图，在菱形ABCD中，AC与BD相交于点O，AC=8，BD=6，则菱形的边长AB=5．