题目内容
20.若点P在x轴上,点A坐标是(2,-1),且PA=3,则点P的坐标是($2+\sqrt{2}$,0)或($2-\sqrt{2}$,0).分析 设出P的坐标,利用两点距离公式,求出P的坐标.
解答 解:由题意设P(x,0),因为PA=3,
$\sqrt{(2-x)^{2}+(-1-0)^{2}}=3$,
解得:x=2+$\sqrt{2}$或x=2-$\sqrt{2}$,
所以点P的坐标为:($2+\sqrt{2}$,0)或($2-\sqrt{2}$,0).
故答案为:($2+\sqrt{2}$,0)或($2-\sqrt{2}$,0)
点评 此题考查坐标与图形问题,关键是两点间距离公式的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列从左到右的变形哪个是分解因式( )
| A. | x2+2x-3=x(x+2)-3 | B. | ma+mb+na+nb=m(a+b)+n(a+b) | ||
| C. | x2-12x+36=(x-6)2 | D. | -2m(m+n)=-2m2-2mn |
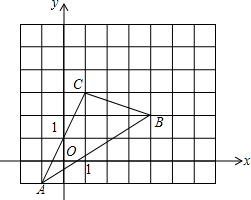 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,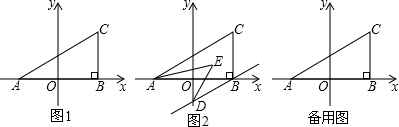
 在平面直角坐标系中,已知点A(0,3)、B(2,1)、C(3,4).
在平面直角坐标系中,已知点A(0,3)、B(2,1)、C(3,4). 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=$\frac{1}{2}$,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=$\frac{1}{2}$,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);