题目内容
5.先化简,再求值:$\frac{x}{2x+3}$÷$\frac{3}{4{x}^{2}-9}$•(1+$\frac{3}{2x-3}$),其中x=-1.分析 根据分式的乘除法和加法可以化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:$\frac{x}{2x+3}$÷$\frac{3}{4{x}^{2}-9}$•(1+$\frac{3}{2x-3}$)
=$\frac{x}{2x+3}×\frac{(2x+3)(2x-3)}{3}×\frac{2x}{2x-3}$
=$\frac{2{x}^{2}}{3}$,
当x=-1时,原式=$\frac{2×(-1)^{2}}{3}$=$\frac{2}{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
16.在方程x+2=0、2x=0、x+y=0、x2=0中,是一元一次方程的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.将分式方程$\frac{x}{x-2}$-$\frac{2}{2-x}$=3化为整式方程,正确的是( )
| A. | x-2=3 | B. | x+2=3 | C. | x-2=3(x-2) | D. | x+2=3(x-2) |
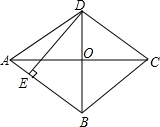 如图,在菱形ABCD中,对角线AC、BD相交于点O,DE⊥AB,垂足为E,如果AC=8,BD=6,那么DE的长为4.8.
如图,在菱形ABCD中,对角线AC、BD相交于点O,DE⊥AB,垂足为E,如果AC=8,BD=6,那么DE的长为4.8.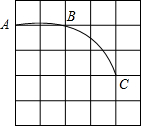 如图,在5×5的正方形网格中,每个小正方形的边长为1,一段圆弧经过格点A、B、C,请完成下列任务.
如图,在5×5的正方形网格中,每个小正方形的边长为1,一段圆弧经过格点A、B、C,请完成下列任务.