题目内容
12．
如图，将两张长为16cm，宽为4cm的矩形纸条交叉，使重叠部分是一个菱形，那么菱形周长的最大值与最小值的和是40．
分析 易知两张纸条垂直时菱形的周长最小；再画出图形，设菱形的边长为x，根据勾股定理求出周长最大值，由此可得到形周长的最大值与最小值的和．
解答 解：当两张纸条如图1所示放置时，菱形周长最大，设这时菱形的边长为xcm，
由勾股定理：x2=（16-x）2+42，
得：2x=17，
∴4x=34，
即菱形的最大周长为34cm．
当两张纸条如图所2示放置时，即是正方形时取得最小值为：4×4=16．
∴菱形周长的最大值与最小值的和是40，
故答案为40．
点评 此题考查的知识点是解直角三角形及菱形的性质，关键是怎样放置纸条使得到的菱形的周长最大，然后根据图形列方程解答．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
3．
若有理数a、b在数轴上的位置如图所示，则下列各式中成立的是（ ）
若有理数a、b在数轴上的位置如图所示，则下列各式中成立的是（ ）| A． | a+b＜0 | B． | a-b＞0 | C． | |a|＜|b| | D． | ab＞0 |
3．
如图，已知△ABC≌△DEF，且AB=5，BC=6，AC=7，则DF的长为（ ）
如图，已知△ABC≌△DEF，且AB=5，BC=6，AC=7，则DF的长为（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 不能确定 |
7．
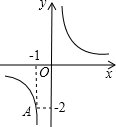如图，反比例函数y=$\frac{k}{x}$的图象经过A（-1，-2），则以下说法错误的是（ ）
如图，反比例函数y=$\frac{k}{x}$的图象经过A（-1，-2），则以下说法错误的是（ ）| A． | k=2 | B． | 图象也经过点B（2，1） | ||
| C． | 若x＜-1时，则y＜-2 | D． | x＞0，y随x的增大而减小 |
在平面直角坐标系xOy中，△ABC的位置如图所示．
1．比-1小1的数是（ ）
| A． | -1 | B． | 1 | C． | 0 | D． | -2 |