Question

4．在平面直角坐标系xOy中，△ABC的位置如图所示．
（1）分别写出△ABC各个顶点的坐标；
（2）判断△ABC的形状，并说明理由；
（3）请在图中画出△ABC关于y轴对称的图形△A′B′C′．

Answer 1

分析 （1）根据平面直角坐标系可得△ABC各个顶点的坐标；
（2）首先利用勾股定理计算出AB、AC、BC长，再利用勾股定理逆定理可证出△ABC为等腰直角三角形；
（3）首先确定A、B、C三点关于y轴对称的对称点位置，然后再连接即可．

解答 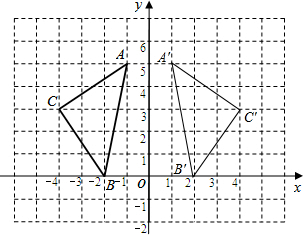解：（1）A（-1，5），B（-2，0），C（-4，3）． 
（2）△ABC为等腰直角三角形． 
理由如下：由勾股定理有：$AB=\sqrt{26}$，$AC=\sqrt{13}$，$BC=\sqrt{13}$
∴AC=BC，AC²+BC²=AB²
∴△ABC为等腰直角三角形．
（3）如图所示．

点评 此题主要考查了作图--轴对称变换，以及勾股定理和勾股定理逆定理，关键是掌握在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方；如果三角形的三边长a，b，c满足a²+b²=c²，那么这个三角形就是直角三角形．