题目内容
3. 如图,一块材料的形状是锐角三角形ABC,边BC=30mm,高AD=20mm,把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上.
如图,一块材料的形状是锐角三角形ABC,边BC=30mm,高AD=20mm,把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上.(1)求证:△AEF∽△ABC;
(2)设线段EG=a,EF=b,求a、b之间的关系式;
(3)当E点运动到何处时,矩形EGHF面积最大?最大面积是多少?
分析 (1)根据矩形的对边平行得到BC∥EF,利用“平行于三角形的一边的直线截其他两边或其他两边的延长线,得到的三角形与原三角形相似”判定即可.
(2)根据相似三角形对应边的比等于对应高的比列出比例式,即可求解;
(3)根据矩形面积公式得到关于a的二次函数,根据二次函数求出矩形的最大值.
解答 解:(1)∵四边形EGHF为矩形,
∴BC∥EF,
∴△AEF∽△ABC;
(2)设线段EG=a,EF=b,
∵△AEF∽△ABC,
∴$\frac{EF}{BC}$=$\frac{AK}{AD}$,$\frac{b}{30}$=$\frac{20-a}{20}$,
∴a、b之间的关系式为b=30-$\frac{3}{2}$a;
(3)∵矩形EGHF面积=ab=a(30-$\frac{3}{2}$a)=-$\frac{3}{2}$a2+30a=-$\frac{3}{2}$(a-10)2+150,
故当a=10,即E点运动到AB的三等分点(靠近A)时,矩形的面积最大,最大面积为150mm2.
点评 本题考查的是相似三角形的应用,利用矩形的面积公式得到关于a的二次函数,根据二次函数的性质,确定a的取值和面积的最大值是解题关键.

练习册系列答案
相关题目
13.下列说法中正确的是( )
| A. | -5的相反数是5 | B. | |m|一定大于0 | C. | -m一定是负数 | D. | |-m|的倒数是$\frac{1}{m}$ |
14.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水.据测试,拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升.小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后水龙头滴下的水为(用科学记数法表示)( )
| A. | 1440毫升 | B. | 1.4×103毫升 | C. | 0.14×104毫升 | D. | 14×102毫升 |
11.已知分式$\frac{2xy}{x-y}$中的x、y的值分别扩大为原来的5倍,则此分式的值( )
| A. | 变为原来的5倍 | B. | 变为原来的10倍 | C. | 变为原来的$\frac{1}{5}$ | D. | 不变 |
8.已知某种花粉的直径为0.000 000 000 254米,则0.000 000 000 254用科学记数法可表示为( )
| A. | 25.4×10-9 | B. | 2.54×10-10 | C. | 2.54×10-8 | D. | 2.54×109 |
15.已知关于x,y的方程xm-2+4ym+n=6是二元一次方程,则m,n的值为( )
| A. | m=1,n=0 | B. | m=3,n=-4 | C. | m=1,n=-2 | D. | m=3,n=-2 |
 完成下面的证明:
完成下面的证明: 如图,已知AD∥BC,A,B,E在一条直线上,∠1=60°,∠2=45°,则∠A=60°,∠BDA=75°.
如图,已知AD∥BC,A,B,E在一条直线上,∠1=60°,∠2=45°,则∠A=60°,∠BDA=75°.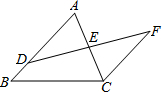 已知:如图,△ABC中,点D,E分别在AB,AC上,CF∥AB交DE的延长线于点F,DE=EF,DB=3,CF=5,则AB=8.
已知:如图,△ABC中,点D,E分别在AB,AC上,CF∥AB交DE的延长线于点F,DE=EF,DB=3,CF=5,则AB=8.