题目内容
20. 已知反比例函数y=$\frac{m-3}{x}$的图象的一支位于第一象限.
已知反比例函数y=$\frac{m-3}{x}$的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为10,求m的值.
分析 (1)根据反比例函数的图象是双曲线.当k>0时,则图象在一、三象限,且双曲线是关于原点对称的;
(2)由对称性得到△OAC的面积为5.设A(x、$\frac{m-3}{x}$),则利用三角形的面积公式得到关于m的方程,借助于方程来求m的值.
解答 解:(1)根据反比例函数的图象关于原点对称知,该函数图象的另一支在第三象限,且m-3>0,则m>3;
(2)∵点B与点A关于x轴对称,若△OAB的面积为10,
∴△OAC的面积为10.
设A(x,$\frac{m-3}{x}$),
则$\frac{1}{2}$x•$\frac{m-3}{x}$=10,
解得:m=23.
点评 本题考查了反比例函数的性质、图象,反比例函数图象上点的坐标特征等知识点.根据题意得到△OAC的面积是解题的关键.

练习册系列答案
相关题目
12.实数-5,0,-$\sqrt{2}$,3中最大的数是( )
| A. | -5 | B. | 0 | C. | -$\sqrt{2}$ | D. | 3 |
10.若a-b=$\frac{1}{2}$,且a2-b2=$\frac{1}{4}$,则a+b的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
 如图,矩形ABCD中,点B与原点重合,点D(8,6),AE⊥BD,△AEB沿着y轴翻折得到△AFB,将△AFB绕着点B顺时针旋转α(0°<α<90°)得到△BF′A′,直线F′A′与线段AB、AE分别交于点M、N,当MN=MA时,△BF′A′与△AEB重叠部分的面积为$\frac{108}{25}$.
如图,矩形ABCD中,点B与原点重合,点D(8,6),AE⊥BD,△AEB沿着y轴翻折得到△AFB,将△AFB绕着点B顺时针旋转α(0°<α<90°)得到△BF′A′,直线F′A′与线段AB、AE分别交于点M、N,当MN=MA时,△BF′A′与△AEB重叠部分的面积为$\frac{108}{25}$. 反比例函数y=$\frac{k}{x}$的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,那么k的值是-6.
反比例函数y=$\frac{k}{x}$的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,那么k的值是-6.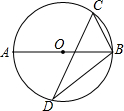 如图,AB为⊙O的直径,∠CDB=30°,则∠CBA=60°.
如图,AB为⊙O的直径,∠CDB=30°,则∠CBA=60°. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).