题目内容
20.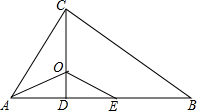 如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC.
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC.(1)求证:△AOC≌△A0E;
(2)求证:OE∥BC.
分析 (1)由角平分线的定义可知∠CAO=∠EAO,依据SAS证明△AOC≌△A0E即可;
(2)由全等三角形的性质可知∠ACO=∠AEO,根据等角的余角相等可知∠DCB=∠DOE,从而可证明OE∥BC.
解答 解:(1)∵AO平分∠BAC,
∴∠CAO=∠EAO.
在△ACO和△AEO中$\left\{\begin{array}{l}{AC=AE}\\{∠CAO=∠EAO}\\{AO=AO}\end{array}\right.$,
∴△AOC≌△A0E.
(2)∵△AOC≌△A0E,
∴∠ACO=∠AEO.
又∵∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,
∴∠DCB=∠DOE.
∴OE∥BC.
点评 本题主要考查的是全等三角形的性质和判定、平行线的判定,利用等角的余角相等证得∠DCB=∠DOE是解题的关键.

练习册系列答案
相关题目
8.已知$\frac{b+c}{a}$=$\frac{a+c}{b}$=$\frac{a+b}{c}$=k,则k的值是( )
| A. | -1 | B. | 2 | C. | -1或2 | D. | 无法确定 |
15.解方程$\frac{x}{x-5}$=3+$\frac{5}{x-5}$的结果( )
| A. | x=5 | B. | x=4 | C. | x=1 | D. | 无解 |

 如图,分别用三个大写字母表示以M为顶点的角.
如图,分别用三个大写字母表示以M为顶点的角.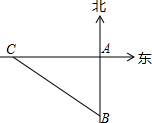 如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.
如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km. 线段BD上有一点C,分别以BC、CD为边作等边三角形ABC和等边三角形ECD,连接BE交AC于M,连接AD交CE于N,连接MN,求证:
线段BD上有一点C,分别以BC、CD为边作等边三角形ABC和等边三角形ECD,连接BE交AC于M,连接AD交CE于N,连接MN,求证: