题目内容
11. 线段BD上有一点C,分别以BC、CD为边作等边三角形ABC和等边三角形ECD,连接BE交AC于M,连接AD交CE于N,连接MN,求证:
线段BD上有一点C,分别以BC、CD为边作等边三角形ABC和等边三角形ECD,连接BE交AC于M,连接AD交CE于N,连接MN,求证:(1)∠1=∠2;
(2)CM=CN;
(3)△CMN为等边三角形.
分析 (1)根据等边三角形的性质得到∠ACD=∠BCE=60°,AC=DC,EC=BC,推出∠ACE=∠DCB,证得△ACE≌△DCB(SAS),根据全等三角形的性质即可得到结论;
(2)由于∠ACD=∠BCE=60°,得到∠DCE=60°,求得∠ACD=∠MCN=60°,证得△ACM≌△DCN(ASA),根据全等三角形的性质即可得到结论;
(3)根据平角的定义得到∠MCN=180°-∠MCA-∠NCB=180°-60°-60°=60°,于是得到结论.
解答 解:(1)∵△ACD和△BCE是等边三角形,
∴∠ACD=∠BCE=60°,AC=DC,EC=BC,
∴∠ACD+∠DCE=∠DCE+∠ECB,
即∠ACE=∠DCB,
在△ACE与△DCB中,
$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{EC=BC}\end{array}\right.$,
∴△ACE≌△DCB(SAS),
∴∠1=∠2;
(2)∵∠ACD=∠BCE=60°,
∴∠DCE=60°,
∴∠ACD=∠MCN=60°,
在△ACM与△DCN中,
$\left\{\begin{array}{l}{∠1=∠2}\\{DC=AC}\\{∠DCE=∠ACD}\end{array}\right.$,
∴△ACM≌△DCN(ASA),
∴CM=CN;
(3)∵∠MCN=180°-∠MCA-∠NCB=180°-60°-60°=60°,
∵CM=CN;
∴△CMN是等边三角形,
点评 本题考查了全等三角形的判定和性质,等边三角形的性质和判定,证得△ACE≌△DCB是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
6. 如图所示,过y轴负半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=-$\frac{6}{x}$和y=$\frac{1}{x}$的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为( )
如图所示,过y轴负半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=-$\frac{6}{x}$和y=$\frac{1}{x}$的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为( )
 如图所示,过y轴负半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=-$\frac{6}{x}$和y=$\frac{1}{x}$的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为( )
如图所示,过y轴负半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=-$\frac{6}{x}$和y=$\frac{1}{x}$的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为( )| A. | $\frac{7}{2}$ | B. | 7 | C. | $\frac{5}{2}$ | D. | 5 |
3.下列语句中,正确的是( )
| A. | 长度相等的弧是等弧;等弧对等弦 | |
| B. | 在同一平面上的三点确定一个圆 | |
| C. | 直径是弦;半圆是劣弧 | |
| D. | 三角形的外心到三角形三个顶点的距离相等 |
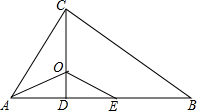 如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC.
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC. 如图所示.线段OB,OC,OA的长度分别是1,2,3.且OC平分∠AOB.若将点A表示为(3,20°),点B表示为(1,110°).则点C可表示为(2,65°).
如图所示.线段OB,OC,OA的长度分别是1,2,3.且OC平分∠AOB.若将点A表示为(3,20°),点B表示为(1,110°).则点C可表示为(2,65°). 如图,点O在直线AB上,∠AOC=∠DOE=90°,OB平分∠EOF,若∠BOF=32°,求∠AOD和∠COE的度数.
如图,点O在直线AB上,∠AOC=∠DOE=90°,OB平分∠EOF,若∠BOF=32°,求∠AOD和∠COE的度数.