题目内容
已知一个直角三角形两条直角边之差是1,斜边长为5,则这个直角三角形的面积等于 .
考点:勾股定理
专题:
分析:设较短的一个直角边长为x,则另一直角边的长为:x+1,根据勾股定理可求得两直角边的长,再根据面积公式求得三角形的面积即可.
解答:解:设较短的一个直角边长为x,则另一直角边的长为:x+1.
由勾股定理得:x2+(x+1)2=52.
解得:x=3.
则x+1=4.
这个直角三角形的面积为:
×3×4=6.
故答案为:6.
由勾股定理得:x2+(x+1)2=52.
解得:x=3.
则x+1=4.
这个直角三角形的面积为:
| 1 |
| 2 |
故答案为:6.
点评:此题主要考查学生对勾股定理的理解及三角形面积公式,关键是根据题意利用勾股定理求出两条直角边的长.

练习册系列答案
相关题目
若a4+3a2=1,b2-3b=1,且a2b≠1,则
的值是( )
| a2b+1 |
| a2 |
| A、3 | B、2 | C、-3 | D、-2 |

 如图,P是同心圆中大圆上的一点,PBA是小圆的割线,若PA•PB=10,则图中圆环的面积是
如图,P是同心圆中大圆上的一点,PBA是小圆的割线,若PA•PB=10,则图中圆环的面积是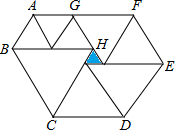 如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为1cm,现欲将此图案的周边镶上一根彩线,问彩线至少需要多长?
如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为1cm,现欲将此图案的周边镶上一根彩线,问彩线至少需要多长?