题目内容
11. 如图,点P是⊙O外一点,PA是⊙O的切线,点A是切点,点B是⊙O上一点,且PA=PB,延长BO分别与⊙O,切线PA的延长线相交于C,Q两点.
如图,点P是⊙O外一点,PA是⊙O的切线,点A是切点,点B是⊙O上一点,且PA=PB,延长BO分别与⊙O,切线PA的延长线相交于C,Q两点.(1)求证:PB是⊙O的切线;
(2)点D为PB的中点,QD交AB于点E,若⊙O的半径为9,OQ=15,求$\frac{AE}{BE}$的值.
分析 (1)连接PO,证明△PAO与△PBO全等即可;
(2)设OP与AB交于点F,连接DF,则DF为△PAO中位线;根据勾股定理算出AQ,进而算出PB、PA,接着算出AE与EF之比,AE与BE之比也就自然可知了.
解答 解:(1)如图1,连接PO,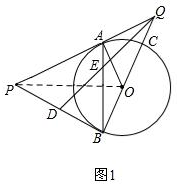
∵PA是⊙O的切线,A是切点,
∴OA⊥PA,
在△PAO和△PBO中,
$\left\{\begin{array}{l}{PA=PB}\\{PO=PO}\\{OA=OB}\end{array}\right.$,
△PAO≌△PBO(SSS),
∴∠ABO=∠PAO=90°,
∴PB是⊙O的切线;
(2)如图2,设OP与AB交于点F,连接DF,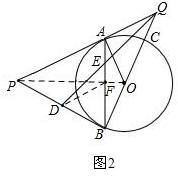
则OP垂直平分AB,
∴F为AB中点,
∵D为PB中点,
∴DF∥PA,DF=$\frac{1}{2}PA$,
∵OA=9,OQ=15,
∴AQ=12,
∵∠QBP=∠QAO=90°,
∴△QPB∽△POA,
∴$\frac{BQ}{PB}=\frac{AQ}{OA}=\frac{12}{9}=\frac{4}{3}$,
∴PB=18,
∴PQ=30,
∴PA=18,
∵DF∥PQ,
∴$\frac{AE}{EF}=\frac{AQ}{DF}=\frac{12}{9}=\frac{4}{3}$,
∵AF=BF,
∴$\frac{AE}{BE}=\frac{2}{5}$.
点评 本题考查了圆的切线的判定与性质、全等三角形的判定与性质、中位线、勾股定理、相似三角形的判定与性质等知识点,难度中等.熟悉切线的判定定理、性质定理是解答的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
2.若a=b,则下列等式中:①a+3=b+3;②2a=2b;③a+1=b-1成立的有( )个.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
16.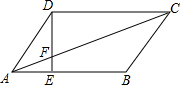 如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD为( )
如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD为( )
 如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD为( )
如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD为( )| A. | 3 | B. | 27 | C. | 6 | D. | 12 |
20.在同一个圆中,四条半径将圆分割成扇形A,B,C,D的面积之比为2:3:3:4,则最大扇形的圆心角为( )
| A. | 80° | B. | 100° | C. | 120° | D. | 150° |
1.如果线段AB=5cm,BC=3cm,那么A,C两点之间的距离为( )
| A. | 8cm | B. | 2cm | ||
| C. | 2cm或8cm | D. | 不小于2cm且不大于8cm |
 图中有几个角3,用字母可以表示为∠BOA,∠COB,∠COA,其中∠AOB可以用数字表示为∠1,∠2可以用字母表示为∠COB.
图中有几个角3,用字母可以表示为∠BOA,∠COB,∠COA,其中∠AOB可以用数字表示为∠1,∠2可以用字母表示为∠COB.