题目内容
10.有一条弧长为2$\sqrt{2}$cm的弧,该弧所对的圆心角为60度,则这条弧所在的圆的半径为$\frac{6\sqrt{2}}{π}$cm.分析 根据弧长公式l=$\frac{nπR}{180}$求出半径.
解答 解:∵l=$\frac{nπR}{180}$,
∴R=$\frac{180×2\sqrt{2}}{60π}$=$\frac{6\sqrt{2}}{π}$.
故答案为:$\frac{6\sqrt{2}}{π}$.
点评 本题考查了弧长的计算,解答本题的关键是掌握弧长公式:l=$\frac{nπR}{180}$.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | 3a+4b=7ab | B. | 7a-3a=4 | C. | 3ab-2ab=ab | D. | 3a+2a=5a2 |
2.计算:72°22′+50°40′30″的结果是( )
| A. | 122°62′30″ | B. | 123°2′30″ | C. | 122°2′30″ | D. | 123°12′30″ |
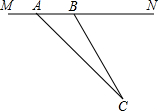 目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.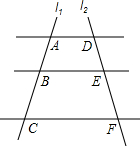 如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为6.
如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为6. 如图是规格为8×8的正方形网格,每个小方格都是边长为1的正方形,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,每个小方格都是边长为1的正方形,请在所给网格中按下列要求操作: