题目内容
 如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点的坐标是(4,3).
如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点的坐标是(4,3).(1)求抛物线的解析式;
(2)将直线l绕点C顺时针旋转90°,交x轴于点Q,y轴上有一点P(0,t),过点P作x轴的平行线交AC于点M,交CQ于点N,设MN的长度为y,求y与t之间的函数关系式;
(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.
考点:二次函数综合题
专题:
分析:(1)利用待定系数法求二次函数解析式解答即可;
(2)利用待定系数法求出直线AC的解析式,然后求出直线l绕点C顺时针旋转90°后的解析式,得出y与t之间的函数关系式;
(3)根据直线AC的解析式,设出过点E与AC平行的直线,然后与抛物线解析式联立消掉y得到关于x的一元二次方程,利用根的判别式△=0时,△ACE的面积最大,然后求出此时与AC平行的直线,然后求出点E的坐标,并求出该直线与x轴的交点F的坐标,再求出AF,再根据直线l与x轴的夹角为45°求出两直线间的距离,再求出AC间的距离,然后利用三角形的面积公式列式计算即可得解.
(2)利用待定系数法求出直线AC的解析式,然后求出直线l绕点C顺时针旋转90°后的解析式,得出y与t之间的函数关系式;
(3)根据直线AC的解析式,设出过点E与AC平行的直线,然后与抛物线解析式联立消掉y得到关于x的一元二次方程,利用根的判别式△=0时,△ACE的面积最大,然后求出此时与AC平行的直线,然后求出点E的坐标,并求出该直线与x轴的交点F的坐标,再求出AF,再根据直线l与x轴的夹角为45°求出两直线间的距离,再求出AC间的距离,然后利用三角形的面积公式列式计算即可得解.
解答:解:(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),
∴
,
解得:
,
所以,抛物线的解析式为y=x2-4x+3;
(2)如图1,
设直线AC的解析式为y=kx+b(k≠0),
则
,
解得:
,
所以,直线AC的解析式为y=x-1,
∵将直线l绕点C顺时针旋转90°,
∴设直线QC的解析式为:y=-x+d,
将(4,3)代入得;3=-4+d,
解得:d=7,
故直线QC的解析式为:y=-x+7,
∵P(0,t),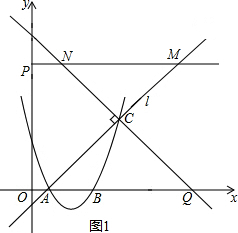 当t>3时,
当t>3时,
则M(x,t),N(x1,t),故t=x+7,t=-x1+7,
则x=t-7,x1=7-t,
故MN=t-7-(7-t)=2t-14,
设MN的长度为y,故y与t之间的函数关系式为:y=2t-14;
同理可得;当t<3时,
则M(x,t),N(x1,t),故t=x+7,t=-x1+7,
则x=t-7,x1=7-t,
故MN=(7-t)-(t-7)=-2t+14,
设MN的长度为y,故y与t之间的函数关系式为:y=-2t+14,
当t=3,则y=0,
综上所述:当t>3时,y与t之间的函数关系式为:y=2t-14;
当t<3时,y与t之间的函数关系式为:y=-2t+14,
当t=3,则y=0;
(3)如图2,设过点E与直线AC平行线的直线为y=x+m,
联立
,
消掉y得,x2-5x+3-m=0,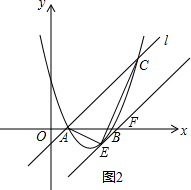
△=(-5)2-4×1×(3-m)=0,
即m=-
时,点E到AC的距离最大,△ACE的面积最大,
此时x=
,y=
-
=-
,
∴点E的坐标为(
,-
),
设过点E的直线与x轴交点为F,则F(
,0),
∴AF=
-1=
,
∵直线AC的解析式为y=x-1,
∴∠CAB=45°,
∴点F到AC的距离为AF•sin45°=
×
=
,
又∵AC=
=3
,
∴△ACE的最大面积=
×3
×
=
,此时E点坐标为(
,-
).
∴
|
解得:
|
所以,抛物线的解析式为y=x2-4x+3;
(2)如图1,
设直线AC的解析式为y=kx+b(k≠0),
则
|
解得:
|
所以,直线AC的解析式为y=x-1,
∵将直线l绕点C顺时针旋转90°,
∴设直线QC的解析式为:y=-x+d,
将(4,3)代入得;3=-4+d,
解得:d=7,
故直线QC的解析式为:y=-x+7,
∵P(0,t),
 当t>3时,
当t>3时,则M(x,t),N(x1,t),故t=x+7,t=-x1+7,
则x=t-7,x1=7-t,
故MN=t-7-(7-t)=2t-14,
设MN的长度为y,故y与t之间的函数关系式为:y=2t-14;
同理可得;当t<3时,
则M(x,t),N(x1,t),故t=x+7,t=-x1+7,
则x=t-7,x1=7-t,
故MN=(7-t)-(t-7)=-2t+14,
设MN的长度为y,故y与t之间的函数关系式为:y=-2t+14,
当t=3,则y=0,
综上所述:当t>3时,y与t之间的函数关系式为:y=2t-14;
当t<3时,y与t之间的函数关系式为:y=-2t+14,
当t=3,则y=0;
(3)如图2,设过点E与直线AC平行线的直线为y=x+m,
联立
|
消掉y得,x2-5x+3-m=0,

△=(-5)2-4×1×(3-m)=0,
即m=-
| 13 |
| 4 |
此时x=
| 5 |
| 2 |
| 5 |
| 2 |
| 13 |
| 4 |
| 3 |
| 4 |
∴点E的坐标为(
| 5 |
| 2 |
| 3 |
| 4 |
设过点E的直线与x轴交点为F,则F(
| 13 |
| 4 |
∴AF=
| 13 |
| 4 |
| 9 |
| 4 |
∵直线AC的解析式为y=x-1,
∴∠CAB=45°,
∴点F到AC的距离为AF•sin45°=
| 9 |
| 4 |
| ||
| 2 |
9
| ||
| 8 |
又∵AC=
| 32+(4-1)2 |
| 2 |
∴△ACE的最大面积=
| 1 |
| 2 |
| 2 |
9
| ||
| 8 |
| 27 |
| 8 |
| 5 |
| 2 |
| 3 |
| 4 |
点评:本题考查了二次函数综合题以及待定系数法求二次函数解析式,待定系数法求一次函数解析式,联立两函数解析式求交点坐标,利用平行线确定点到直线的最大距离问题.

练习册系列答案
相关题目
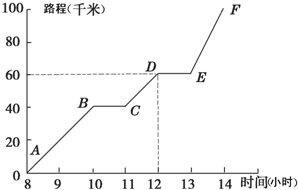 如图,描述了小明早晨8时到下午14时,骑摩托车从甲地到乙地所走路程与时间的关系,根据折线图提供的信息思考下列问题:?
如图,描述了小明早晨8时到下午14时,骑摩托车从甲地到乙地所走路程与时间的关系,根据折线图提供的信息思考下列问题:? 如图,在平面直角坐标系中,动点P从点A(0,10)出发,以3个单位/秒的速度沿y轴向点O匀速运动,动点Q从点B(5,0)同时出发,以1单位/秒的速度沿x轴向点O匀速运动,当其中一个点到达终点时,另一点也停止运动.设运动的时间为t秒.以P、Q为圆心作⊙P和⊙Q,且⊙P和⊙Q的半径分别为4和1.
如图,在平面直角坐标系中,动点P从点A(0,10)出发,以3个单位/秒的速度沿y轴向点O匀速运动,动点Q从点B(5,0)同时出发,以1单位/秒的速度沿x轴向点O匀速运动,当其中一个点到达终点时,另一点也停止运动.设运动的时间为t秒.以P、Q为圆心作⊙P和⊙Q,且⊙P和⊙Q的半径分别为4和1. 如图,AD∥BE∥CF,直线a、b与这三条平行线分别交于点A、B、C和点D、E、F,AB=4,BC=6,DE=3,则EF的长是( )
如图,AD∥BE∥CF,直线a、b与这三条平行线分别交于点A、B、C和点D、E、F,AB=4,BC=6,DE=3,则EF的长是( )