题目内容
已知|x|+|x-1|=|x-2|+|x-3|,求x的值.
考点:含绝对值符号的一元一次方程
专题:
分析:根据x取值范围分类讨论,即可求得x的值,即可解题.
解答:解:①x≥3,则原式化简为x+x-1=x-2+x-3,无解;
②2≤x<3,则原式化简为x+x-1=x-2+3-x,解得x=1,不符合题意;
③1≤x<2,则原式化简为x+x-1=2-x+3-x,解得x=
,符合题意;
④0≤x<1,则原式化简为x+1-x=2-x+3-x,解得x=2,不符合题意;
⑤x<0,则原式化简为-x+1-x=2-x+3-x,无解;
综上所述x的值为
.
②2≤x<3,则原式化简为x+x-1=x-2+3-x,解得x=1,不符合题意;
③1≤x<2,则原式化简为x+x-1=2-x+3-x,解得x=
| 3 |
| 2 |
④0≤x<1,则原式化简为x+1-x=2-x+3-x,解得x=2,不符合题意;
⑤x<0,则原式化简为-x+1-x=2-x+3-x,无解;
综上所述x的值为
| 3 |
| 2 |
点评:本题考查了含绝对值符号的一元一次方程的求解,本题中分类讨论并验证x的值是否符合题意是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将4.34059精确到千分位是( )
| A、4.341 |
| B、4.34 |
| C、4.3406 |
| D、4.340 |
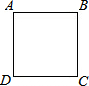 如图,沿着边长为90cm的正方形,按照A-B-C-D-A…的方向,电子蚂蚁甲从A以65cm/min的速度前进,电子蚂蚁乙同时从A以72cm/min的速度前进.
如图,沿着边长为90cm的正方形,按照A-B-C-D-A…的方向,电子蚂蚁甲从A以65cm/min的速度前进,电子蚂蚁乙同时从A以72cm/min的速度前进.